Luku 2.1 (7th Grade Mathemathics)

Natural numbers

  • Numbers and digits
  • Writing and comparing numbers
  • Natural numbers
  • Calculations with natural numbers
Lisää aiheesta
Muut toiminnot

The history of numerals

India

Indian mathematicians were already using the numbers 1-9 three hundred years before the common era. They already understood very large numbers and the concept of infinity. The number zero is known from the Bakhshali manuscript found in 1881 in a village of the same name. In early texts, mathematical relationships were explained verbally, and the word śūnya meant zero.

Baghdad

Indian numerals arrived in Baghdad around 800 CE, when a scientist called al-Horazmi began to write books on mathematics. This led to the spread of numerical notation around the world.

England

The English monk Adelad (c. 1100 CE) translated the works of al-Horazmi. He wrote the book Liber algorismi de numero indorum and was one of the first people in Europe to use Arabic numerals.

North Africa

Italian traders visited North Africa in the Middle Ages. In 1202, the Italian mathematician Fibonacci introduced his well-known Fibonacci sequence to the world.

The digits we use today originate from India. They reached Europe through the Arabian peninsula, which is why they are called Arabian numerals.
Lisää aiheesta
Muut toiminnot

Numbers and digits

Numbers and digits

  • Numerical digits are symbols used to write numbers.
  • Numbers are used to mark quantities or amounts.
  • In the decimal system, ten different digits are used to form numbers:

0, 1, 2, 3, 4, 5, 6, 7, 8, 9,

  • The meaning of a digit depends on its position in the number.
  • An infinite number of numbers can be formed from digits.

Number

Name

Explanation

1 000 000

  thousand

1 000 000 000

 thousand

1 000 000 000 000

  thousand


Smallest possible number

Largest possible number

2 digits

3 digits

4 digits

5 digits

Lisää aiheesta
Muut toiminnot

Natural numbers

The natural numbers 0, 1, 2, 3, ... belong to a set of numbers called the set of natural numbers. This set of numbers is denoted by the letter ℕ.

ℕ = {0, 1, 2, 3, ...} 

Natural numbers have evolved from the need to count quantities of objects.

  • A natural number is even if it ends in
    ​number 0, 2, 4, 6 or 8.
  • A natural number is odd if it ends in
    ​number 1, 3, 5, 7 or 9.

Example 1

Addition and multiplication

  • When two natural numbers are added together, the result is always a natural number.
  1. 112 + 354 = 466
  1. 39 + 0 = 39
  • When two natural numbers are multiplied by each other, the result is always a natural number.
  1. 12 ⋅ 6 = 72
  1. 39 ⋅ 0 = 0

Subtraction and division

  • When a natural number is subtracted from another natural number, the result is not always a natural number.

112 – 354 = –242 is not a natural number.

  • When a natural number is divided by another natural number, the result is not always a natural number.

21 : 6 = 3,5 is not a natural number.

Note

Addition and subtraction of even numbers

  • The sum of two even numbers is always an even number.

22 + 24 = 46

  • The difference between two even numbers is always an even number.

24 – 22 = 4

Addition and subtraction of odd numbers

  • The sum of two odd numbers is always an even number.

21 + 23 = 44

  • The difference between two odd numbers is always an even number.

25 – 21 = 4

Addition and subtraction of even and odd numbers

  • The sum of an even number and an odd number is always an odd number.

22 + 21 = 43

  • The difference of an even number and an odd number is always an odd number.

33 – 22 = 11

  1. Write the smallest natural number. 
  2. Write the smallest two-digit number and subtract 1 from it. What number do you get?
      − 1 = 
  3. Write the highest three-digit number and add 1 to it. What number do you get?
      + 1 = 
  4. The natural number n is followed by the number .
  5. The natural number n is preceded by the number  .

For the curious

2 + 2 – 2 – 2 : 2 = 1

2 2 2 2 2 = 1

2 + 2 + 2 – 2 – 2 = 2

2 2 2 2 2 = 2

2 2 22 2 = 3

2 2 22 2 = 3

2 2 22 2 = 4

2 2 22 2 = 4

2 2 22 2 = 5

2 2 22 2 = 5

2 2 22 2 = 6

2 2 22 2 = 6

2 2 22 2 = 7

2 2 22 2 = 7

2 2 22 2 = 8

2 2 22 2 = 8

2 2 22 2 = 9

2 2 22 2 = 9

2 2 22 2 = 10

2 2 22 2 = 10

Lisää aiheesta
Muut toiminnot

Practise and solve

Number

Sum of the digits

681

7 935

Number

Sum of the digits

48 903

627 352

Large numbers

Write the numbers with digits. 

Over the course of one month, the average person breathes
six hundred and forty-seven thousand eight hundred and fifty
() times.

Exhaled air becomes visible in cold weather.

Over the course of one lifetime, the heart beats approximately
two billion five hundred million
() times.

The size and location of the human heart.

Every day,
one hundred and seventy-two billion eight hundred million
() new red blood cells are produced in the human body.

A blood sample on a glass slide under a microscope.

Read and think

Answer the following verbal tasks. Find the information you need in the text. Reflect and make notes if necessary. Solve the question by calculating. See the last slide for hints on solutions.

The bakery sold bread to three stores. 54 kg was sold to the first store and 21 kg to the the second. The third store bought 27 kg more bread than the first. How much bread was sold to the third store?

  kg of bread was sold to the third store.

A blacksmith was supposed to use 53 kg of iron in his forge, but in fact 12 kg less than that was used. How much iron was actually worked?

The blacksmith used  kg of iron.

38 grain loads have been weighed at the weighing station. That is 12 loads more than there are loads still waiting to be weighed. How many loads will be weighed in total?

In total,  grain loads will be weighed.

Hints for the solutions
Lisää aiheesta
Muut toiminnot

Good to know

23 607 812

23 607 802

490 294

409 294

6 298 006

6 289 006

50 376 985

50 376 958

298 348 120 876

3 billion

1000 million

1 billion

5 000 006

50 000 000

870 056

870 560

Read and think

Answer the following verbal tasks. Find the information you need in the text. Reflect and make notes if necessary. Solve the question by calculating. See the last slide for hints on solutions.

The train has three carriages. The first carriage had 34 passengers and the second 17.

  1. How many passengers were in the third carriage, knowing that there were 13 fewer than in the first two carriages combined?
  2. How many passengers were there in all the carriages on the train?

Answers

  1. The third carriage had  passengers.
  2. The train had a total of  passengers.

There were 133 passengers on the southbound train and 203 on the northbound.

  • At the station, 43 passengers were transferred from the southbound train to the northbound one.
  • 76 passengers on the northbound train changed to the southbound train.

How many passengers were there on each train after that?

Answer

The northbound train had  passengers and the southbound train  passengers.

At the first stop, 112 passengers got off the train, while 39 passengers got on board. At the next station, 45 passengers got off the train and 76 got on. The train continued its journey with 178 passengers.

How many passengers were on the train before the first stop?

  • At the stations, the train received   passengers.
  • At the stations,   passengers left the train.

Answer

The train had  passengers before the first stop.

Hints to tasks 1 and 2
Hints to tasks 3 and 4

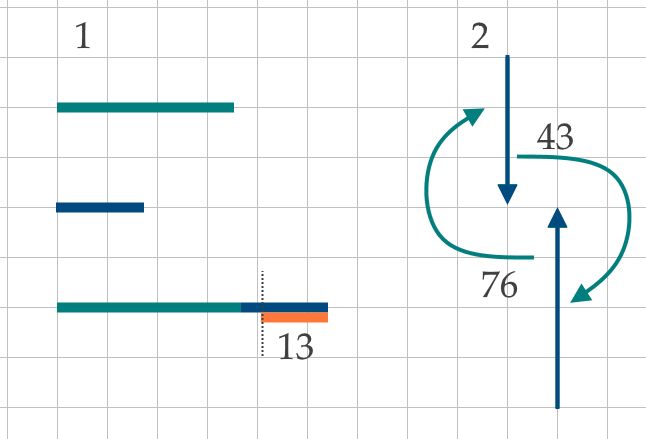
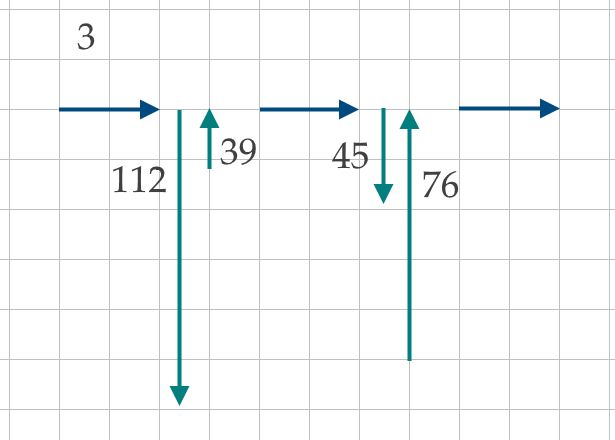
From one number to another

Consider the rule according to which the number in the top row turns to the number in the bottom row. Add the missing numbers.

1

2

3

4

5

6

7

↓

↓

↓

↓

↓

↓

↓

↓

2

3

4

5

6

7

8

1

2

3

4

5

6

7

↓

↓

↓

↓

↓

↓

↓

↓

3

4

5

6

7

8

9

1

2

3

4

5

6

7

↓

↓

↓

↓

↓

↓

↓

↓

2

4

6

8

10

12

14

1

2

3

4

5

6

7

↓

↓

↓

↓

↓

↓

↓

↓

4

6

8

10

12

14

16

Lisää aiheesta
Muut toiminnot

Extra

Magic square

A magic square is a square table where teh numbers in each row (▶), column (▼) and diagonal (◢, ◣) form the same sum.

For example:

▶ 9 + 2 + 7 = 18

▶ 4 + 6 + 8 = 18

▶ 5 + 10 + ? = 18

▼ 9 + 4 + 5 = 18

▼ 2 + 6 + 10 = 18

▼ 7 + 8 + ? = 18

◢ 5 + 6 + 7 = 18

◣ 9 + 6 + ? = 18

Conclusion: The question mark is replaced by the number 3.

Magic square #1

4

9

8

7

3

6

5

Magic number: 

Magic square #2

7

10

11

13

Magic number: 

Magic square #3

5

35

20

45

10

Magic number: 

5 3 1 4 6 8 7 9 4 3 6 4 3 5 7 1 9 2 7 8 5 2 1 4 1 9 2 5 6 1 9 7 7 9 2 5 8 4 4 9 6 5 3 1 8 6 7

Lisää aiheesta
Muut toiminnot
Odota