Keskeisiä kysymyksiä
- Mitä eroa on matkalla ja siirtymällä sekä toisaalta vauhdilla ja nopeudella?
- Miten määritetään keskinopeus?
- Millaista on tasainen liike?
Liikettä havaitaan lukemattomissa luonnonilmiöissä. Maa kiertää Aurinkoa, ihmiset etenevät Maan pinnalla, ja ilmakehän molekyylit liikkuvat jatkuvasti. Liikkeen mittaamiseen tarvitaan yksinkertaisimmillaan jokin pituusmitta ja kello. Näiden avulla voidaan määrittää kappaleen paikka eri hetkillä, ja laskea kappaleen liikettä kuvaavia suureita, kuten nopeutta ja kiihtyvyyttä.
Kappaleen liikkeen määrittämiseksi tarvitaan vertailupiste, jonka suhteen liikettä tutkitaan. Vertailupiste voi olla juoksukilpailun lähtöviiva tai paikka, jonne ollaan matkalla. Vertailupiste paikan koordinaatistossa on origo. Liikkeen aikana paikka origon suhteen muuttuu. Muutos voidaan esittää graafisesti aika-paikka-koordinaatistossa. Tätä esitystapaa kutsutaan paikan kuvaajaksi. Alla olevalla videolla mitataan radio-ohjattavan auton liikettä ultraäänianturilla. Anturi mittaa auton etäisyyden anturiin nähden. Auton lähtöpiste on valittu origoksi ja liikkeen alkusuunta positiiviseksi suunnaksi.
Paikan muutos on siirtymä . Siirtymä lasketaan vähentämällä tarkasteluvälin loppupaikasta tarkasteluvälin alkupaikka . Siirtymä ilmaisee lyhimmän etäisyyden loppu- ja alkupaikan välillä: se on suoraviivainen polku lähtöpisteestä loppupisteeseen. Delta-merkillä ilmaistaan, että kyseessä on paikan muutos, ei paikka.

Koska liike voi tapahtua eri suuntiin, siirtymä voi olla positiivinen tai negatiivinen. Siirtymän merkki määräytyy sen mukaan, miten vertailupisteeseen nähden on liikuttu. Positiivisen suunnan voi valita itse, jos suunnan merkkiä ei ole ennalta määritelty.
Arkikielessä etenemistä kuvataan suureella matka. Siirtymä määrittyy paikan alku- ja loppupisteen perusteella. Näiden pisteiden välillä liikkuva kappale voi todellisuudessa kulkea mielivaltaista polkua pitkin. Matka huomioi kuljetun polun pituuden. Matka kuvaa etenemisen suuruutta ja on aina positiivinen.
Edestakaisessa liikkeessä palataan takaisin lähtöpisteeseen. Tällaista on esimerkiksi hissin liike yläkerrokseen ja takaisin lähtökerrokseen. Jos kahden kerroksen välinen etäisyys on 5 m, hissin kulkema matka edestakaisessa liikkeessä on 10 m. Siirtymä sen sijaan on 0 m, koska hissin paikka lopussa on sama kuin alussa.
Kappaleen siirtymä () on sen paikan muutos: , missä on kappaleen paikka alussa ja paikka lopussa.
Kappaleen kulkeman polun pituus on kappaleen kulkema matka. Matka on aina positiivinen luku.
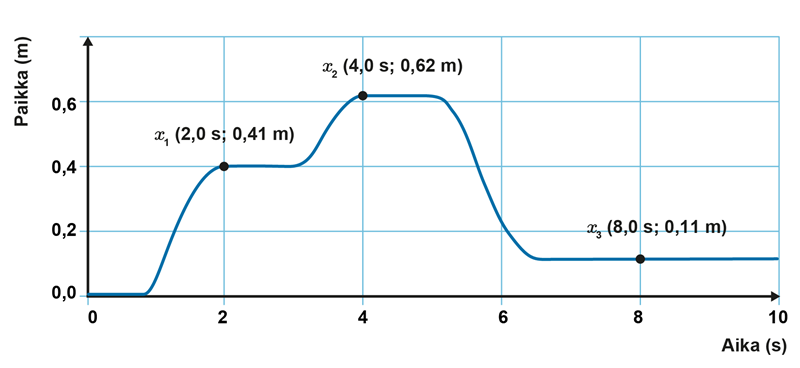
Nopeus kuvaa paikan muutosta ajan suhteen. Liikkeen keskinopeus on siirtymän ja siihen käytetyn ajan suhde. Koska keskinopeuteen vaikuttaa vain siirtymän suuruus ja siihen kulunut aika, tämä ei kerro mahdollisista nopeuden vaihteluista siirtymän aikana. Laskemalla keskinopeus saadaan tietää, millä nopeudella kappale olisi liikkunut, jos se olisi kulkenut vakionopeudella. Keskinopeus voi olla siirtymän tavoin positiivinen tai negatiivinen. Nopeuden merkki kuvaa liikkeen suuntaa koordinaatiston origoon nähden. Määritetään seuraavaksi videolla nähdyn radio-ohjattavan auton liikkeen kuvaajan perusteella siirtymä ja keskinopeus kahdella eri aikavälillä.
Aineisto
Taulukko: Radio-ohjattavan-liike.ods (LibreCalc)
Taulukko: Radio-ohjattavan-liike.cmbl (Logger Pro)
Taulukko: Radio-ohjattavan-liike.cap (Capstone)
Taulukko: Radio-ohjattavan-liike.gambl (Graphical Analysis)
Siirtymä A pisteestä pisteeseen tapahtuu aikavälillä 2,0 s... 4,0 s ja on 0,21 m. Keskinopeus on siis
Siirtymä B pisteestä pisteeseen on -0,51 m ja tapahtuu aikavälillä 4,0 s...8,0 s. Keskinopeus on
Nopeus on liikettä kuvaava suure, joka huomioi liikkeen suuruuden lisäksi suunnan. Vauhti on suure, joka kuvaa ainoastaan liikkeen suuruutta. Radio-ohjattavan auton vauhti on aina positiivinen riippumatta siitä, liikkuuko auto vasemmalle vai oikealle. Keskivauhti lasketaan jakamalla matka siihen kuluneella ajalla: . Vauhdilla ei ole vakiintunutta suuretunnusta. Radio-ohjattavan auton keskivauhti tarkasteluvälillä A on 0,11 m/s ja välillä B 0,13 m/s.
Nopeus on kappaleen paikan muutos ajan suhteen.
Kappaleen keskinopeus () on siirtymä jaettuna siirtymään kuluneella ajalla.
Liikkeen keskivauhti on matka jaettuna siihen kuluvalla ajalla eli . Vauhdilla ei ole vakiintunutta suuretunnusta.

Yksinkertaisin liikkeen malli on tasainen liike. Luonnossa esiintyy paljon liikettä, joka voidaan mallintaa tasaiseksi. Valo etenee tasaisella nopeudella tai junan matkavauhti on likimain tasaista. Tasaista liikettä nähdään myös oheisella videolla, jossa kaksi herkkäliikkeistä vaunua liikkuvat vaunuradalla.
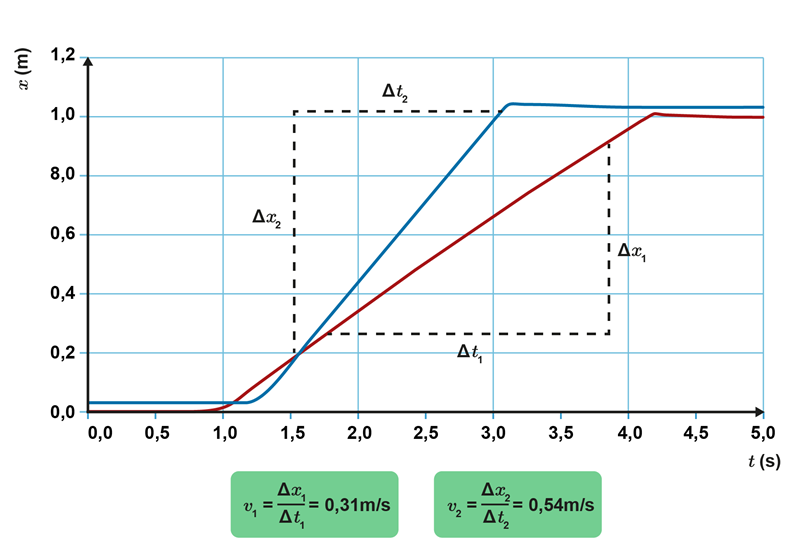
Vaunujen liikkeistä muodostettiin aika-paikka-kuvaajat samaan koordinaatistoon. Liikkeen aikana kuvaajat ovat nousevia suoria. Tämä tarkoittaa, että paikka kasvaa tasaisesti: joka sekunnin aikana paikka muuttuu saman verran. Alla esimerkiksi punaisen vaunun 1 nopeus oli 0,31 m/s, eli se eteni jokaisen sekunnin aikana 0,31 m.
Sinisen vaunun liike oli nopeampaa kuin punaisen. Tämä ilmenee jyrkempänä kuvaajana, eli sinisen vaunun paikka kasvaa nopeammin. Koska nopeus on paikan muutos jaettuna kuluneella ajalla, nopeus on paikan kuvaajan kulmakerroin. Nopeammin kulkevan sinisen vaunun kuvaajan kulmakerroin on suurempi.
Aineisto
Taulukko: Tasainen-liike.ods (LibreCalc)
Taulukko: Tasainen-liike.cmbl (Logger Pro)
Taulukko: Tasainen-liike.cap (Capstone)
Taulukko: Tasainen-liike.gambl (Graphical Analysis)
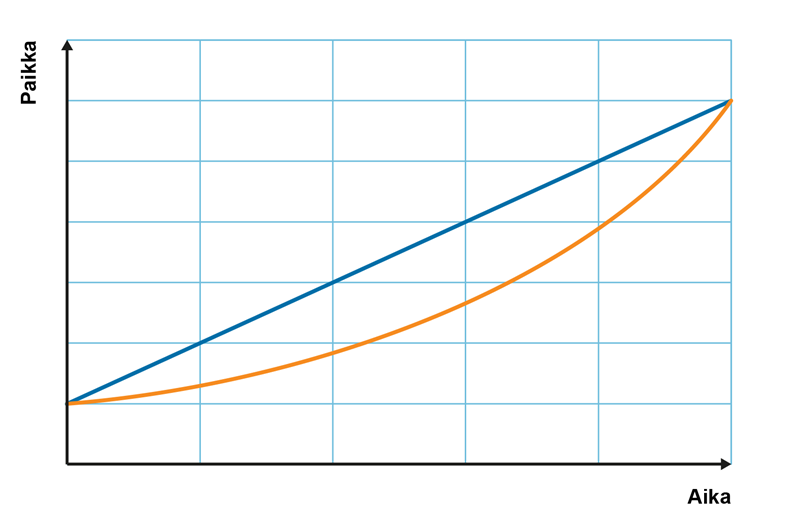
1. Kumman kuvaajan esittämässä liikkeessä siirtymä on suurempi?
2. Kumman kuvaajan esittämän liikkeen keskinopeus koko tarkasteluvälillä on suurempi?
3. Kumman kuvaajan esittämässä liikkeessä nopeus on vakio?
4. Auto liikkuu suoralla tiellä. Mikä seuraavista pitää paikkansa?
Tasaisessa liikkeessä paikan kuvaaja on siis suora. Tämän suoran kulmakerroin ilmaisee kappaleen nopeuden. Tasaisessa liikkeessä kappaleen nopeus on koko ajan sama, joten määritetty nopeus ja keskinopeus ovat sama asia. Kuvaajan kulmakerroin määritetään mittausaineistosta sovittamalla mittauspisteisiin suora sopivalla analysointiohjelmalla.
Origon kautta kulkevan suoran yhtälö on -koordinaatistossa matemaattisesti muotoa , jossa on suoran kulmakerroin. Suoran yleisessä muodossa ilmentää pystyakselia. Paikan kuvaajassa pystyakselilla on suure paikka . Yleisen muodon tekijä ilmentää vaaka-akselia. Paikan kuvaajassa vaaka-akselilla on suure aika . Kulmakerroin on liikkeen nopeutta kuvaava suure. Täten tasaista liikettä kuvaava matemaattinen malli on muotoa olettaen, että se on tarkastelun alkuhetkellä origossa.
Jos tasaisesti liikkuva kappale ei ole origossa hetkellä , paikan yhtälö on , missä on paikka tarkastelun alkuhetkellä.
Tasaisessa liikkeessä nopeus (, engl. velocity) on vakio. Nopeus määritetään tasaisessa liikkeessä aika-paikka-kuvaajan kulmakertoimena. Tasaisen liikkeen nopeuden matemaattinen malli on
Tasaisessa liikkeessä kappaleen paikka lasketaan lausekkeella
Sekunti on joihinkin arkielämän liiketilanteisiin lyhyt aika ja metri lyhyt matka. Liikenteessä matkaa mitataan kilometreissä ja aikaa tunneissa. Nopeuden lisäyksikkö on km/h. Yksikkömuunnokset voidaan tehdä seuraavalla tavalla:
ja
Muutos m/s → km/h
Muutos km/h → m/s
Koehenkilö käveli käytävällä. Henkilön paikkaa mitattiin ultraäänianturilla. Mittaustulokset on esitetty ohessa eri tiedostomuodoissa. Muodosta tai avaa henkilön aika-paikka-kuvaaja, ja vastaa sen perusteella seuraaviin kysymyksiin.
Aineisto
Taulukko: Kavelynopeus.ods (LibreCalc)
Taulukko: Kavelynopeus.cmbl (Logger Pro)
Taulukko: Kavelynopeus.cap (Capstone)
Taulukko: Kavelynopeus.gambl (Graphical Analysis)
a.
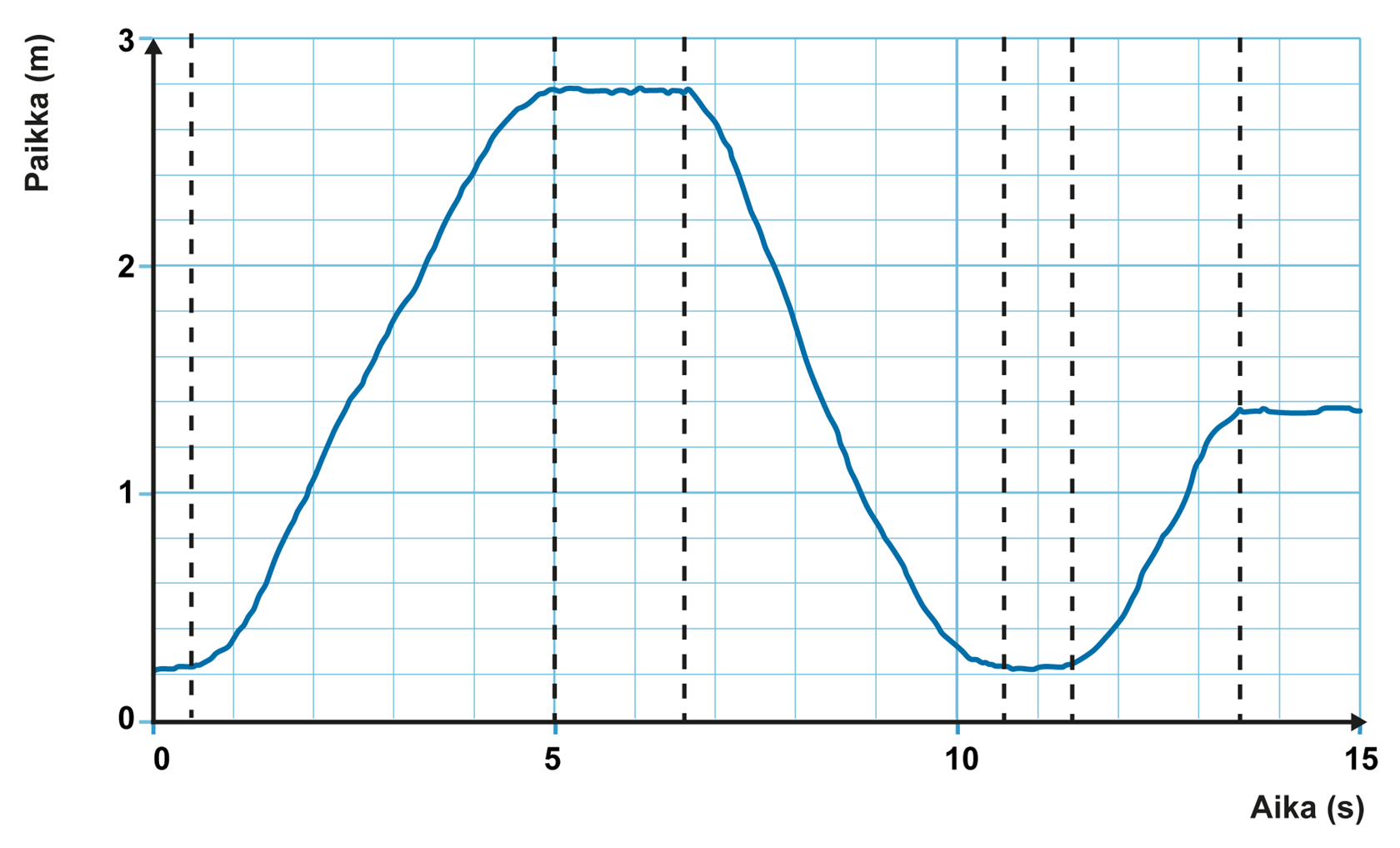
Henkilö liikkuu eteenpäin liikkeen paikan kuvaajan ollessa nouseva ja taaksepäin kuvaajan laskiessa. Kuvaajan perusteella henkilö liikkui eteenpäin aikaväleillä 0,5...5 s ja 11,5...13,5 s.
Välillä 6,5...10,5 s henkilö liikkui taaksepäin.
Oheiseen kuvaajaan on merkitty pystyviivoin hetket, jolloin henkilö lähtee liikkeelle tai pysähtyy.
Henkilö liikkui eteenpäin aikaväleillä 0,5...5 s ja 11,5...13,5 s. Välillä 6,5...10,5 s henkilö liikkui taaksepäin.
b. Siirtymä koko mittauksen aikana on loppupaikan ja alkupaikan erotus eli 1,3 m – 0,2 m = 1,1 m.
Matka saadaan laskemalla edestakaisten siirtymien suuruudet (itseisarvot) yhteen. Matka on siis
Siirtymä koko mittauksen aikana on 1,1 m ja kuljettu matka 6,1 m.
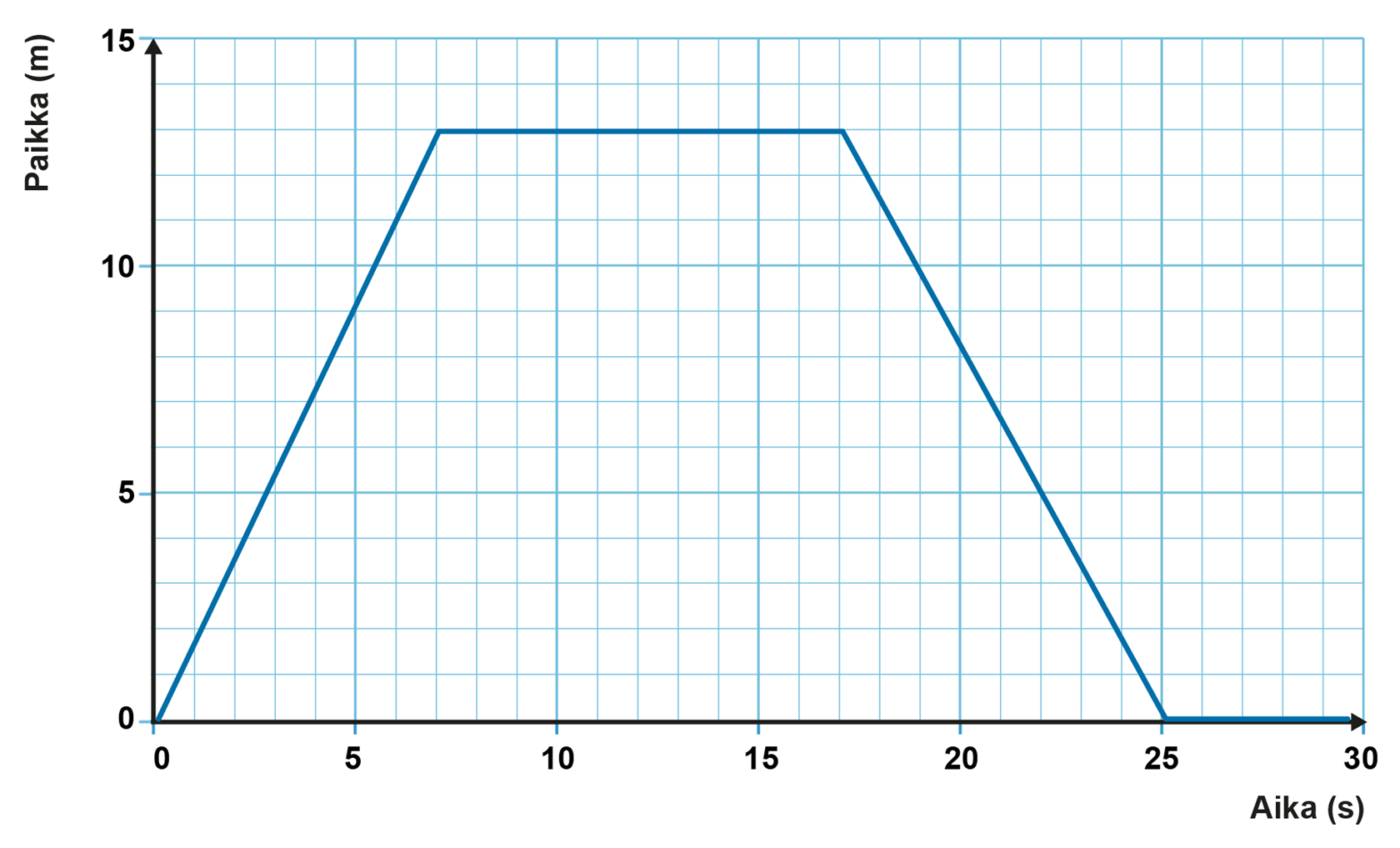
Lue tarvittavat lukuarvot kuvaajasta ja määritä
a. Siirtymä:
Matka:
b. Keskinopeus saadaan nopeuden ja ajan arvoilla välin päätepisteistä laskemalla.
c. Hetkellä 20 s kuvaaja on suora eli liike on tasaista. Nopeus lasketaan suoran kulmakertoimena.
a. Keskinopeus voidaan laskea käyttäen yksiköitä kilometri ja tunti. Aikaa Helsingistä Lahteen kuluu 51 minuuttia, joka on tunneissa
Keskinopeus on
b. Ratkaistaan keskinopeuden määritelmästä aika
Käytetään keskinopeudesta arvoa 124,71 km/h (välitulos, enemmän merkitseviä numeroita kuin lopullisessa vastauksessa):
Juna on Kouvolassa klo 17.36.
Avaa vähintään 10 metriä pitkä mittanauha suoraksi käytävän lattialle. Ajanottajat asettuvat mitan varrelle metrin välein. Ajanottajien kellot käynnistetään yhtä aikaa, ja yksi henkilö kävelee mitattavan matkan. Ajanottajat pysäyttävät kellonsa, kun kävelijä ohittaa heidät. Saadaan kävelyn väliajat yhden metrin välein, jotka kirjataan yhteiseen dokumenttiin. Toistetaan mittaus muutamalla henkilöllä. Esitetään liikkeet kuvaajina aika-paikka-koordinaatistossa. Lasketaan kävelyjen keskinopeudet. Olivatko kävelyt tasaista liikettä?
Asenna mittanauha pystysuuntaan ja pudota höyhen niin, että näet sen sijainnin pystysuunnassa mittanauhasta. Pudota höyhen ja kuvaa video pudotuksesta. Määritä videon perusteella höyhenen paikka sopivin aikavälein ja esitä tulokset aika-paikka-koordinaatistossa. Oliko höyhenen liike tasaista? Jos oli, määritä höyhenen putoamisnopeus.
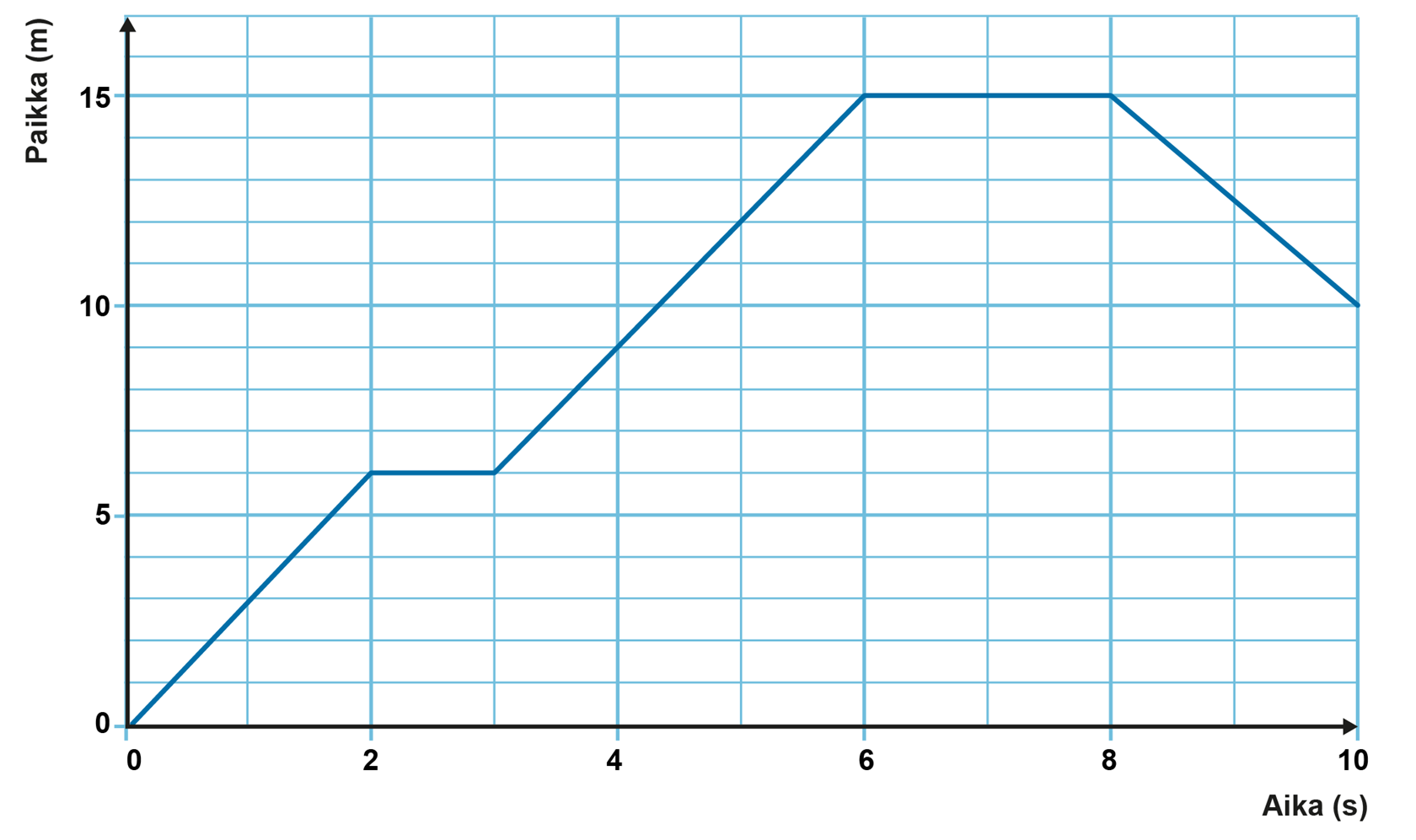
1. Mikä on opiskelijan paikka hetkellä 2,0 s?
Anna vastaus kokonaislukuna:metriä.
2. Kuinka suuri on opiskelijan siirtymä välillä 0...10 s?
Anna vastaus kokonaislukuna: metriä.
3. Kuinka suuri on opiskelijan kulkema matka välillä 0...10 s?
Anna vastaus kokonaislukuna: metriä.
4. Kuinka suuri on opiskelijan keskinopeus välillä 0...10 s?
Anna vastaus kokonaislukuna: metriä sekunnissa.
5. Kuinka suuri on opiskelijan nopeus välillä 3...6 s?
Anna vastaus kokonaislukuna: metriä sekunnissa.
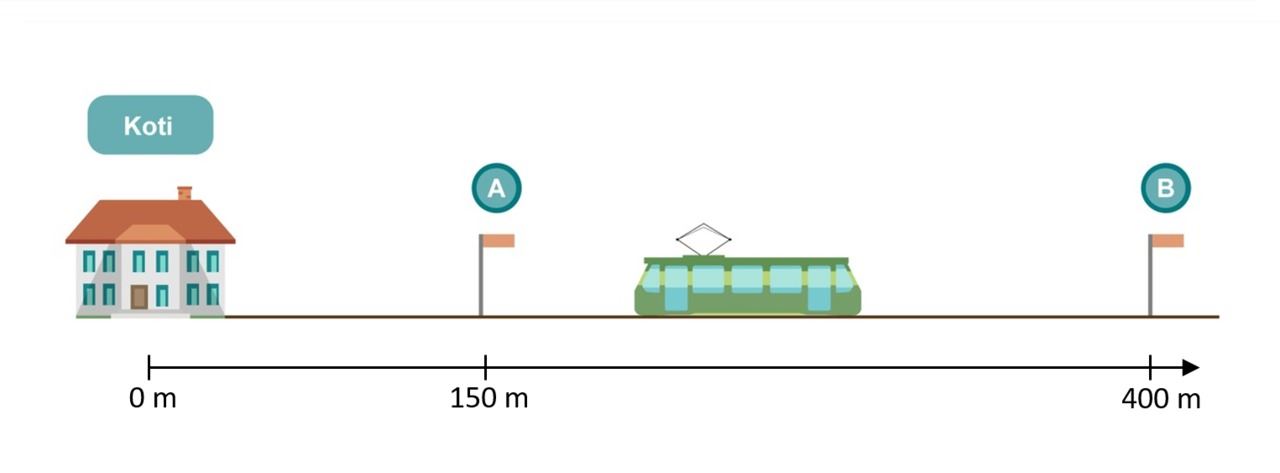
1. Masa juoksee kotoaan 24 sekunnissa pysäkille A . Kuinka suuri on hänen keskinopeutensa kahden numeron tarkkuudella?
Vastaus: m/s.
2. Masa matkustaa raitiovaunun kyydissä pysäkiltä A pysäkille B nopeudella 10 m/s. Kuinka kauan ratikkamatka kestää kahden numeron tarkkuudella?
Vastaus: s.
3. Masa odotti raitiovaunua 45 sekuntia pysäkillä A. Kuinka suuri oli Masan keskinopeus koko matkalla kotoa pysäkille B kahden numeron tarkkuudella?
Vastaus: m/s.
4. Masa palaa kävellen kotiin pysäkiltä B. Kävelyn keskivauhti on 2,5 m/s. Kuinka kauan kotimatka kestää kahden numeron tarkkuudella?
Vastaus: s.
5. Kuinka suuri oli Masan keskinopeus hänen kävellessään kotiin?
Vastaus: m/s.
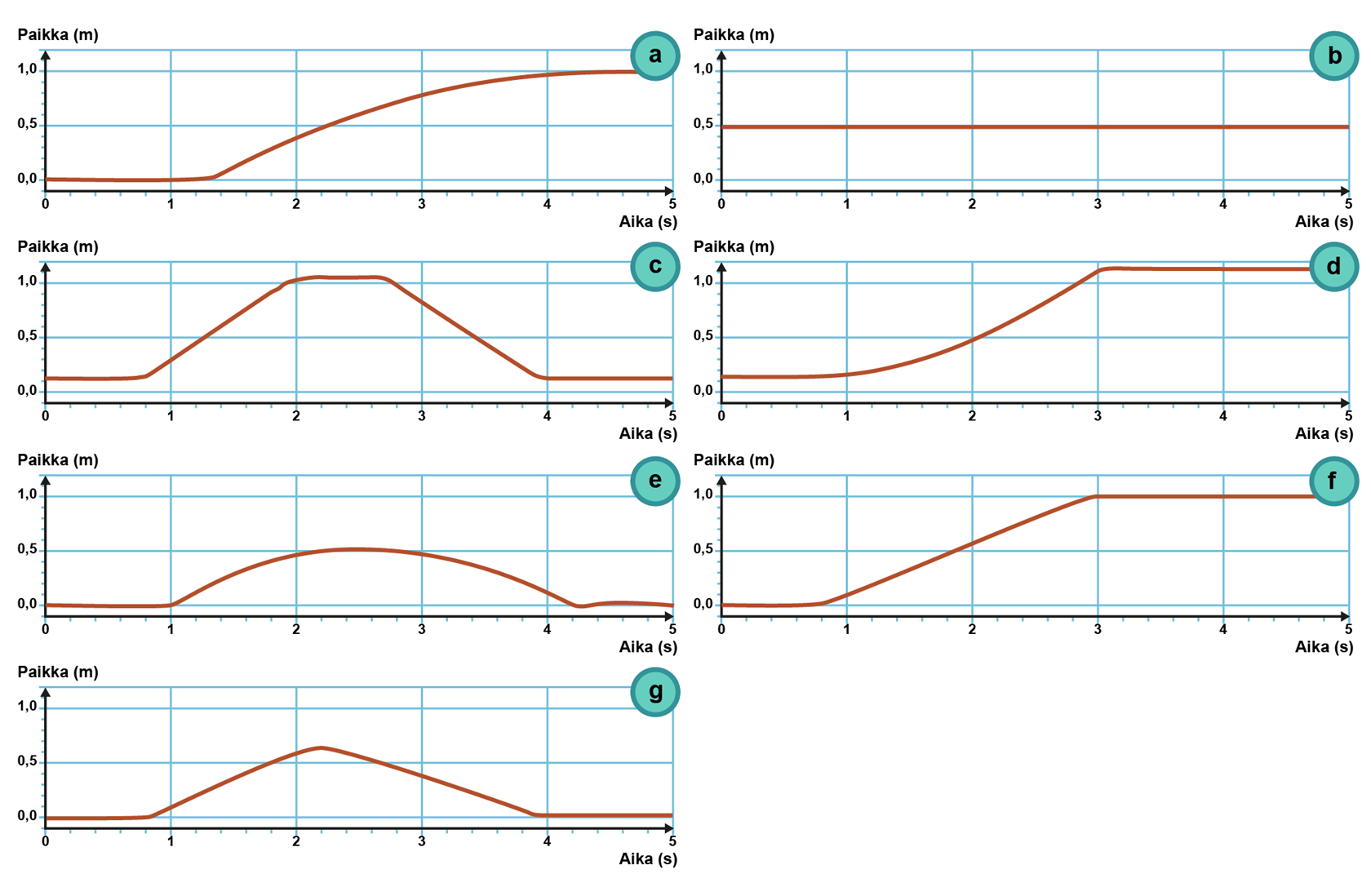
1. Liike 1:
2. Liike 2:
3. Liike 3:
4. Liike 4:
5. Liike 5:

Mitä haluat tehdä tekstillä? Teksti käsitellään tekoälyn avulla, eikä sitä sen jälkeen muokata tai tarkisteta. Tekstissä voi esiintyä virheitä. Tarkista tekstin oikeellisuus vertaamalla sitä kirjan alkuperäistekstiin.
Valitse tiedostot, jotka haluat lisätä. Tuetut formaatit ovat txt, html, htm, pdf, odt, odp, ods, xls, xlsx, ppt, pptx, pps, doc, docx, rtf, png, jpg, jpeg ja gif.
| Nimi | |
|---|---|
| poista |
Huom.! Linkkien tulee alkaa ”http://”!
Opiq käyttää verkkosivun toiminnan, turvallisen käytön varmistamisen, käytön analysoimisen ja parhaan käyttömukavuuden tarjoamisen edellyttämiä evästeitä.
Eväste on käyttäjän tietokoneelta verkkosivun palvelimeen lähetettävä pieni tiedosto, joka sisältää verkkosivun toiminnan edellyttämiä käyttäjää ja hänen tekemiä valintoja koskevia tietoja.
Isoin osa evästeistä ovat Opiqin toiminnan kannalta välttämättömiä. Analyyttisistä evästeistä voi luopua ja silloin ei sinun käyttötietojasi ei käytetä Opiqin kehittämiseen. Lue lisää