Keskeisiä kysymyksiä
- Mitä tarkoitetaan mallilla?
- Miten muodostetaan graafinen malli suureiden välisestä riippuvuudesta?
- Miten tehdään ennusteita graafisen mallin perusteella?
Mallintaminen
Fysiikka on luonnonilmiöiden mallintamista. Malli tarkoittaa yksinkertaistettua esitystä jostakin kappaleesta tai ilmiöstä. Samaa ilmiötä voidaan esittää useilla erityyppisillä malleilla, jotka korostavat ilmiön eri piirteitä.
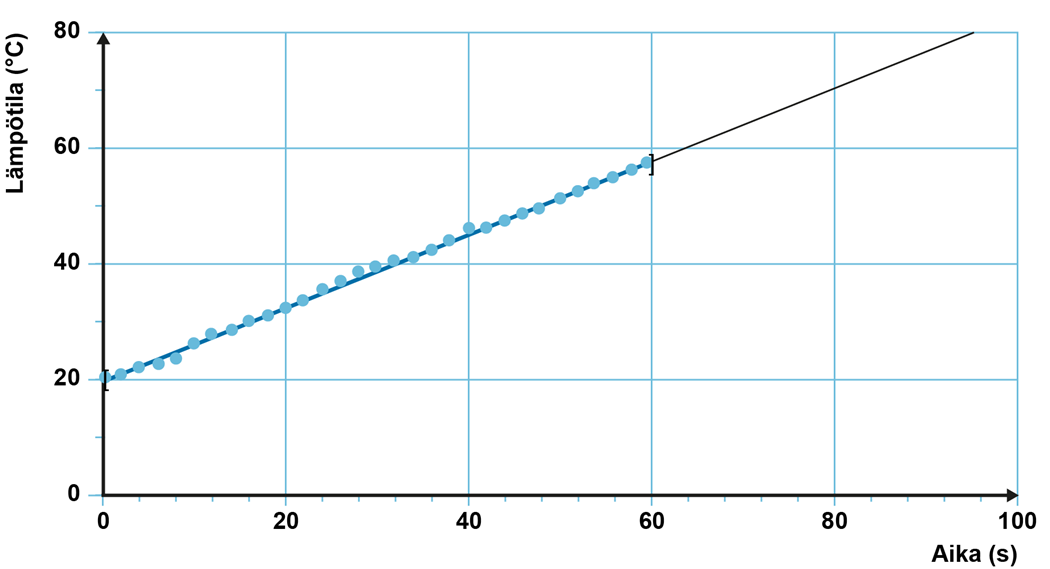
Tarkastellaan esimerkkinä veden lämmittämistä vedenkeittimessä. Veden lämpötilan voidaan havaita nousevan säännönmukaisesti suhteessa aikaan. Lämpötilan ja ajan riippuvuus voidaan esittää kuvaajana eli graafisena mallina.
Kuvaajaa tarkasteltaessa voidaan päätyä matemaattiseen yhtälöön, joka ilmaisee riippuvuuden lämpötilan T ja lämmitykseen kuluneen ajan t välillä. Kyseessä on matemaattinen malli.
Yhtälössä T0 ilmaisee veden lämpötilan lämmityksen alussa. k on keittimen ja veden ominaisuuksista riippuva vakio.
Lämpenevää vettä voidaan toisaalta tarkastella yksittäisten molekyylien tasolla. Lämpötilan nousu ilmenee veden molekyylien voimistuvana liikkeenä. Alla oleva animaatio on malli, joka havainnollistaa ilmiötä mikroskooppisella tasolla.
havainnollistaa esim. mikroskooppisia ilmiöitä visuaalisesti
yksinkertaistus jostakin kappaleesta tai ilmiöstä
riippuvuuden ilmaiseva matemaattinen yhtälö
esim. kuvaaja koordinaatistossa
Mittaustulosten taulukointi ja graafinen esittäminen
Tutkittaessa suureiden välisiä riippuvuuksia suunnitellaan koejärjestely ja mittaus riippuvuuden löytämiseksi. Mittauksen tulokset kirjataan taulukkoon. Taulukossa ilmaistaan mitattu suure nimellä ja tunnuksella. Pelkkää suureen tunnusta voidaan käyttää, mikäli se kertoo yksiselitteisesti mitatun suureen. Taulukko voidaan tehdä mittaustulosten käsittelyyn soveltuvalla ohjelmistolla tai taulukkolaskentaohjelmalla.
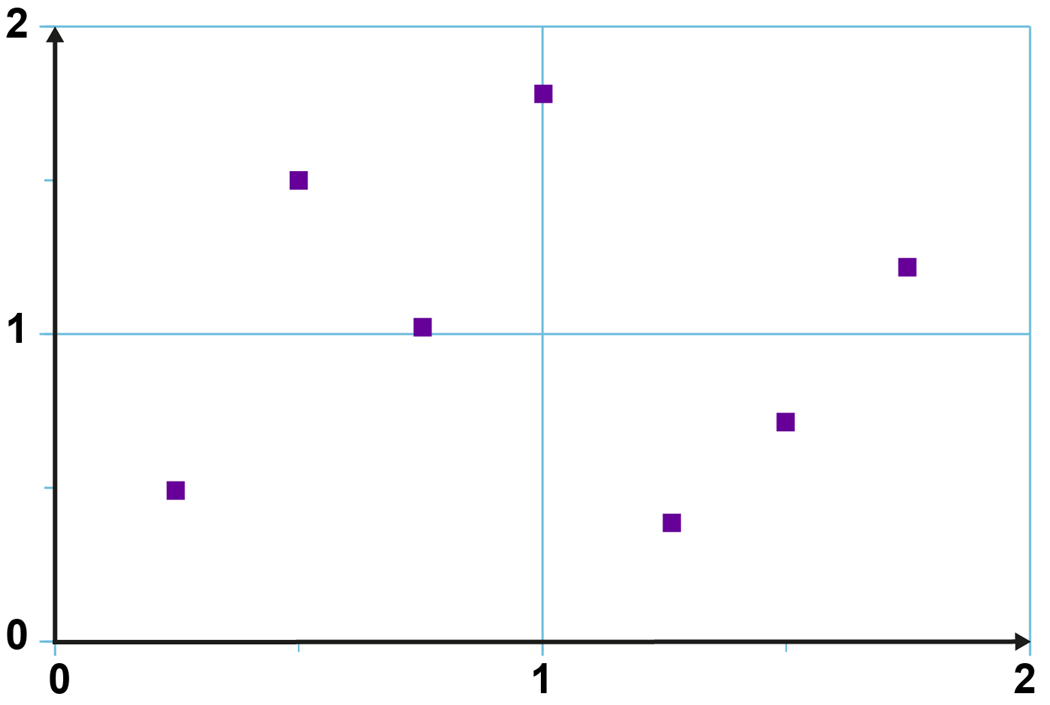
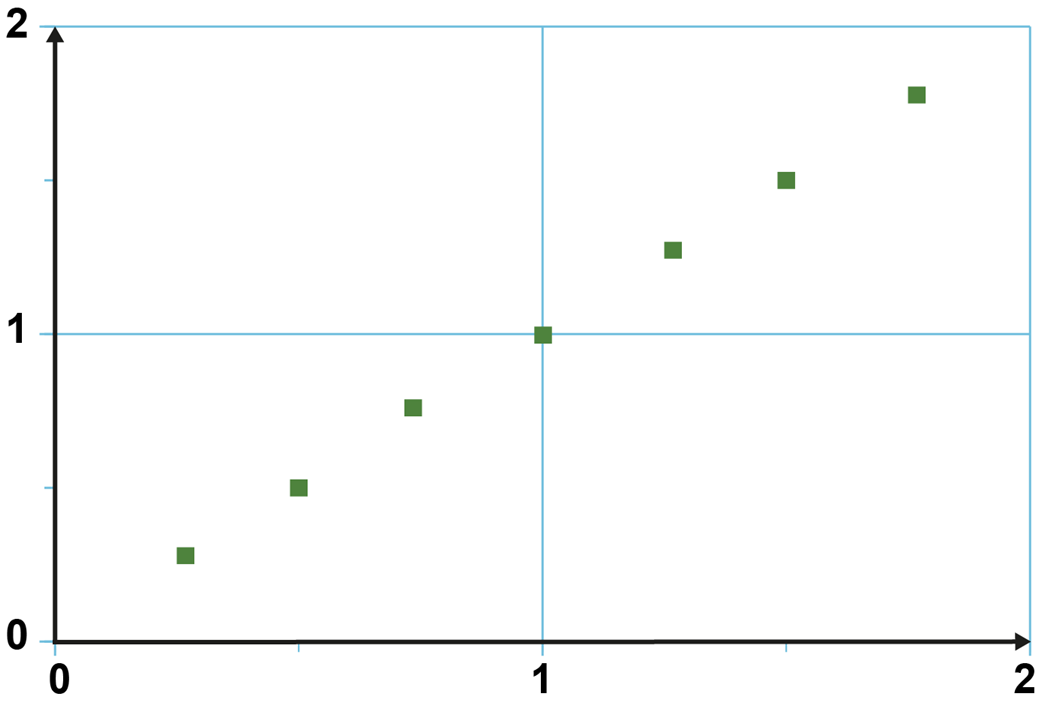
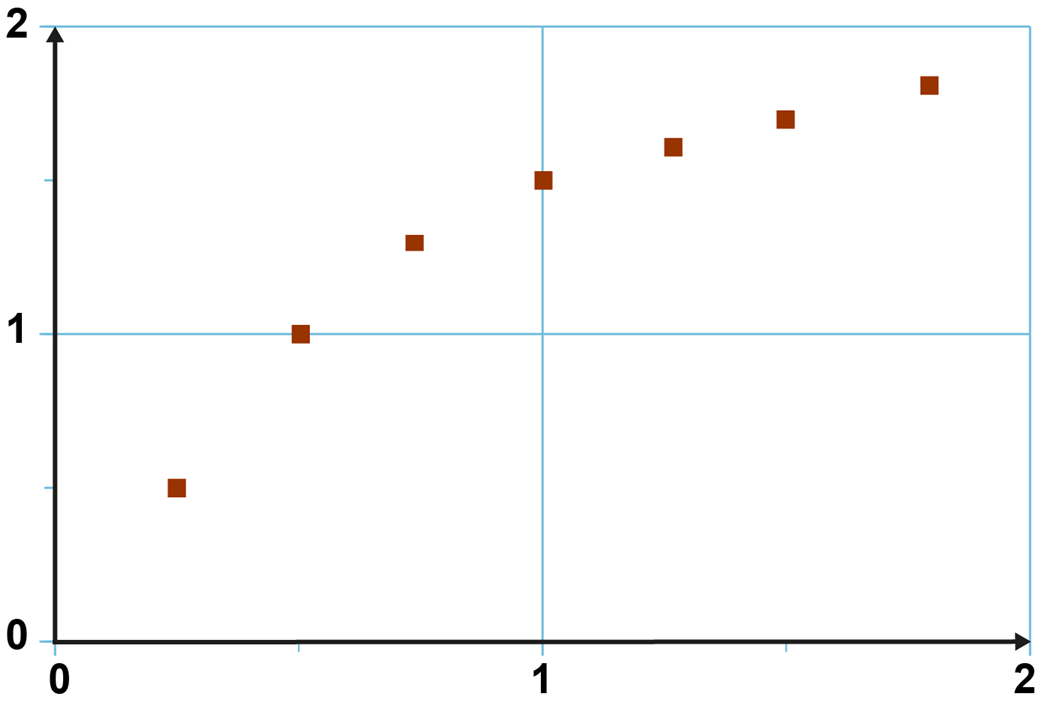
Kahdelle suureelle taulukoidut tulokset esitetään graafisesti koordinaatistossa. Koordinaatiston vaaka-akseli ilmaisee yhden suureen ja pystyakseli toisen. Akseleilla ovat suureen nimi tai tunnus sekä suureen yksikkö. Graafisesta mallista päätellään, onko suureiden välillä säännöllinen riippuvuus ja minkälainen riippuvuus on kyseessä. Riippuvuuden hahmottamiseksi vaaditaan riittävästi mittauspisteitä. Kaksi pistettä on liian vähän, sillä niiden kautta voidaan muodostaa minkämuotoinen käyrä tahansa. Viisi mittauspistettä on kohtuullinen määrä, enemmän on aina parempi. Säännölliseen pistejoukkoon voidaan sovittaa käyrä ja määrittää sen yhtälö.
Esimerkki: Putoavat kappaleet
Koejärjestelyssä tutkittiin paperikartion ja pallon putoamisliikettä. Pudotukset videoitiin ja videoanalyysin avulla määritettiin kappaleiden nopeudet ajan funktiona. Video ja taulukoidut tulokset on esitetty alla.
t (s) | vpallo (m/s) | vkartio (m/s) |
0,02 | 0,47 | 0,403 |
0,1 | 1,05 | 0,961 |
0,18 | 1,837 | 1,556 |
0,26 | 2,645 | 2,183 |
0,34 | 3,522 | 2,643 |
0,42 | 4,524 | 3,04 |
0,5 | 5,283 | 3,422 |
0,58 | 6,102 | 3,746 |
0,66 | 7,116 | 3,963 |
0,74 | 4,328 | |
0,82 | 4,534 |
Mittaustulokset: putoavat kappaleet
Taulukko: Putoavat_kappaleet.ods (LibreCalc)
Taulukko: Putoavat_kappaleet.cmbl (Logger Pro)
Taulukko: Putoavat_kappaleet.cap (Capstone)
Taulukoitujen tulosten perusteella nähdään, että nopeus suurenee ajan putoamisajan kasvaessa, mutta lukuarvoista ei voida suoraan päätellä, missä suhteessa muutos tapahtuu. Tuloksista piirretään kuvaaja. Putoavien kappaleiden nopeus kasvaa ajan kuluessa, joten on luontevaa esittää aika vaaka-akselilla ja nopeus pystyakselilla.
Molemmissa kuvaajissa on havaittavissa säännönmukainen muoto. Nopeudet kasvavat, joten kappaleiden liikettä voidaan kutsua muuttuvaksi ja tarkemmin kuvaten kiihtyväksi. Riippuvuutta mallinnetaan sovitteella. Se on käyrä tai suora, joka mukailee mittauspisteitä. Sovite ei saa peittää mittauspisteitä ja yksittäisten mittauspisteiden on erotuttava edelleen kuvaajassa. Yhdenkään pisteen ei tarvitse osua täsmälleen sovitteelle, koska mittauksiin sisältyy aina virheitä. Osa pisteistä jää sen yläpuolelle ja osa alapuolelle. Paperikartion nopeutta ilmaisee parhaiten käyrä, joka muuttuu ajan kasvaessa loivemmaksi. Pallon nopeus vaikuttaa sen sijaan muodostavan suoran. Kappaleet siis putoavat eri tavoin. Järkeviä sovitteita voi olla useita. Sopivimman vaihtoehdon löytämiseksi vaaditaan tarkempia mittauksia tai taustateoriaa. Jos vaadittavaa teoriaa ei ole tiedossa, silmämääräisesti tehty mielekäs sovite riittää.
Suureiden riippuvuuden esittäminen graafisella mallilla
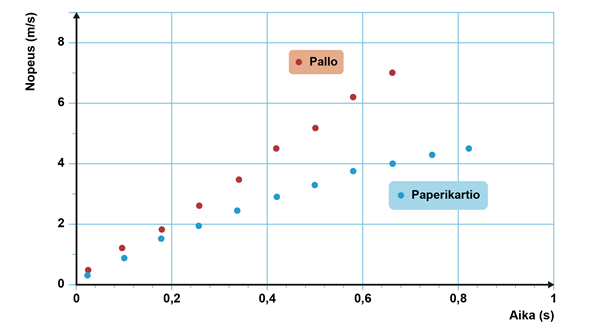
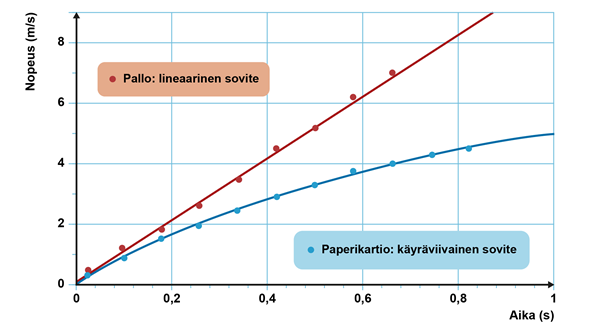
Kahden mitatun suureen riippuvuus esitetään koordinaatistossa siten, että toinen suureista on vaaka-akselin ja toinen pystyakselin muuttuja. Akseleiden otsikoissa ilmoitetaan suureet ja niiden yksiköt. Mittattujen suureiden arvoista syntyy pistejoukko koordinaatistoon. Pistejoukkoa mallinnetaan sovitekäyrällä. Jos suureiden riippuvuus tunnetaan teoreettisesti, käytetään oikeantyyppistä sovitetta, muutoin riittää silmämääräisesti mielekäs sovite.
Ennusteen tekeminen graafisen mallin perusteella
Interpolointi ja ekstrapolointi
Interpolointi tarkoittaa suureen arvon määrittämistä mitattujen arvojen väliltä.
Ekstrapolointi tarkoittaa suureen arvon määrittämistä mittausalueen ulkopuolelta.
Kun suureen arvoja interpoloidaan tai ektstrapoloidaan kuvaajasta, on menetelmä mainittava tulosten raportoinnin yhteydessä. Ekstrapolointi ja interpolointi on mahdollista tehdä myös laskemalla arvoja sovitteen yhtälön perusteella.
Interpolointi
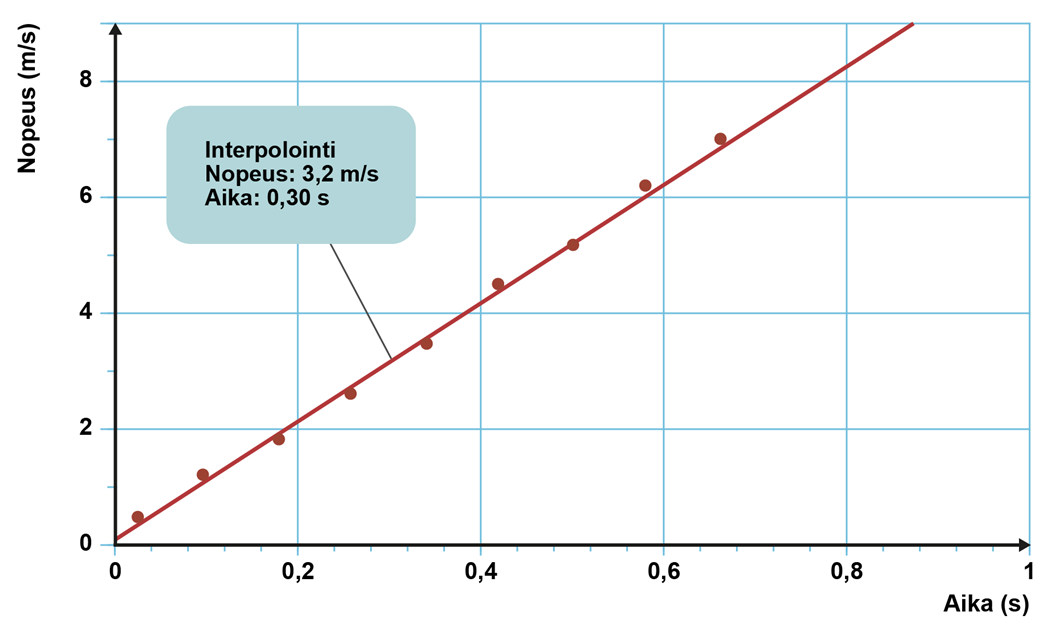
Mallien avulla tehdään ennusteita luonnonilmiöistä. Putoavan pallon nopeus määritettiin muutaman sekunnin kymmenyksen välein, ja mittauspisteet muodostivat likimäärin suoran. On ilmeistä, että nopeus on kasvanut lineaarisesti myös mitattujen pisteiden välissä. Tuloksiin sovitettua suoraa hyödyntäen voidaan arvioida pallon nopeuksia sellaisillakin hetkillä, jolloin nopeutta ei mitattu. Nopeuden arviointia kahden mittauspisteen välissä kutsutaan interpoloinniksi. Alla olevassa kuvaajassa on määritetty pallon nopeudeksi 3,2 m/s hetkellä 0,30 s mittausohjelman interpolointitoiminnon avulla.
Ekstrapolointi
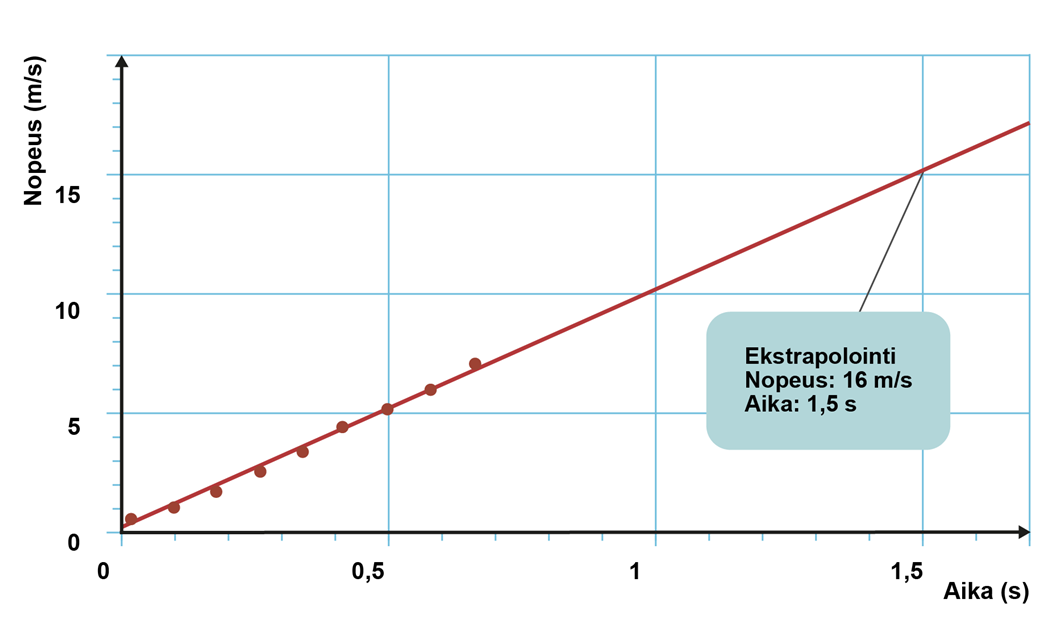
Putoavan pallon nopeuden graafisen mallin perusteella voidaan myös ennustaa pallon nopeutta, jos pallo pudotetaan korkeammalta ja kauemmin kestävän putoamisliikkeen oletetaan jatkuvan samanlaisena. Sovitesuoraa jatketaan mittauspisteiden rajoittaman välin ulkopuolelle ja suoralta luetaan nopeuden arvoja. Menetelmää kutsutaan ekstrapoloinniksi. Alla olevassa kuvaajassa on ekstrapoloimalla arvioitu pallon nopeudeksi 16 m/s, kun se on pudonnut 1,5 s sekunnin ajan.
Ekstrapolointi on järkevää vain silloin, kun mitattu ilmiö oletetaan samanlaiseksi mittausalueen ulkopuolella. Putoavan pallon tapauksessa ekstrapolointi on luotettavaa muutama sekunti eteenpäin. Pidempikestoisten mittausten tai taustateorian perusteella voidaan osoittaa, että putoaminen ei jatku samanlaisena useita kymmeniä sekunteja. Tämä tarkoittaa, että lineaarisen mallin pätevyysalue on rajallinen.
Esimerkit
Esimerkki 1
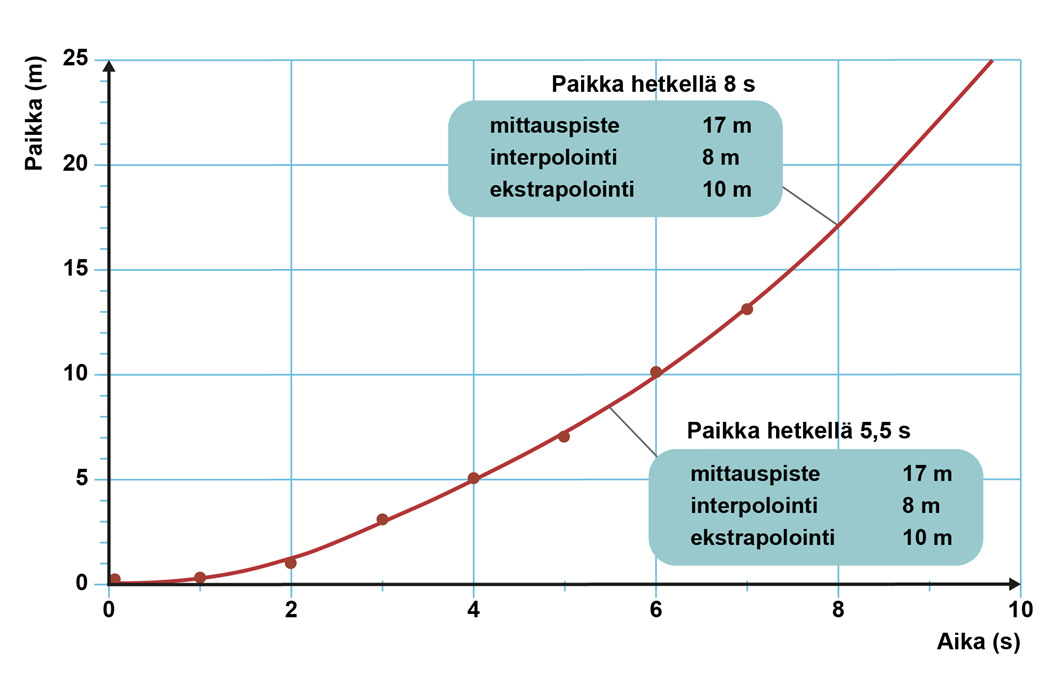
Äänilähteen intensiteettitasoa mitattiin eri etäisyyksillä desibelimittarilla. Tulokset olivat seuraavanlaiset.
Etäisyys (m) | 1,0 | 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | 7,0 |
Intensiteettitaso (dB) | 91 | 86 | 84 | 80 | 78 | 77 | 72 |
- Esitä graafisesti intensiteettitason riippuvuus etäisyydestä.
- Arvioi kuvaajan perusteella intensiteettitaso 1,5 metrin etäisyydellä.
- Arvioi kuvaajan perusteella intensiteettitaso 10,0 metrin etäisyydellä.
Esimerkin 1 ratkaisu
a.
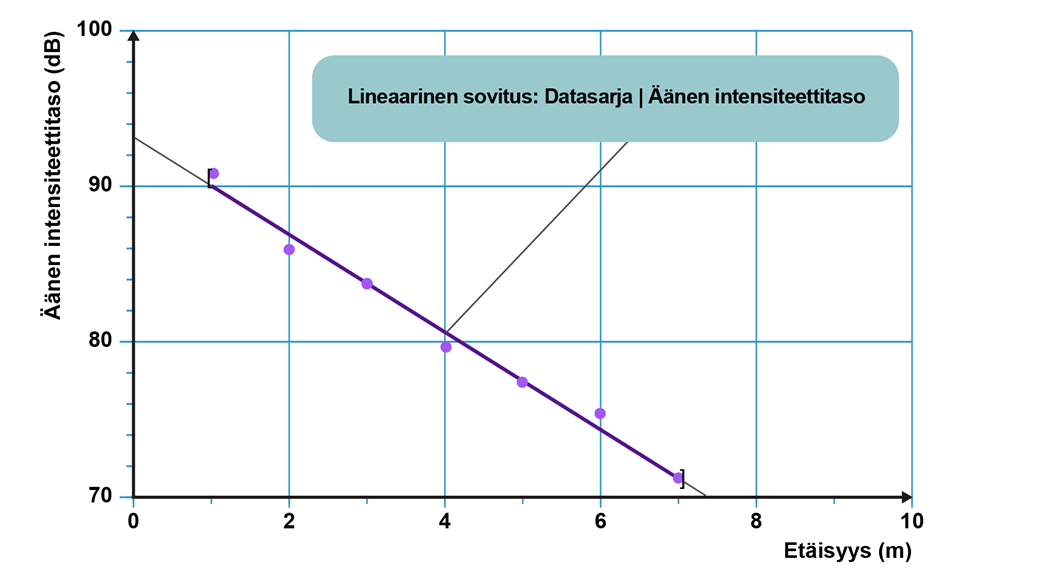
Intensiteettitason riippuvuus etäisyydestä esitettynä graafisesti.
b.
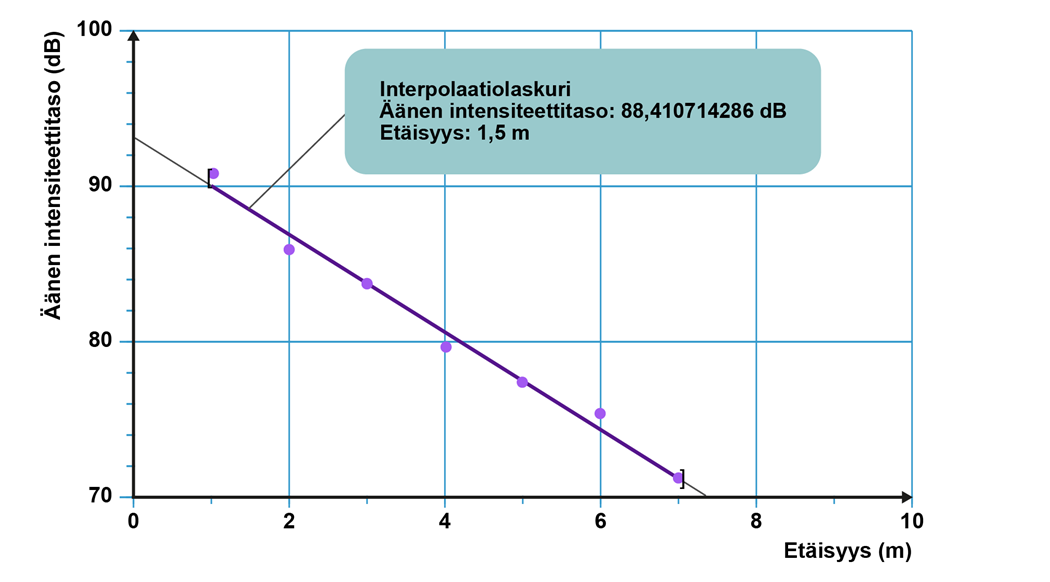
Kuvaajaa interpoloimalla havaitaan, että 1,5 metrin etäisyydellä intensiteettitaso on n. 88 dB.
c.
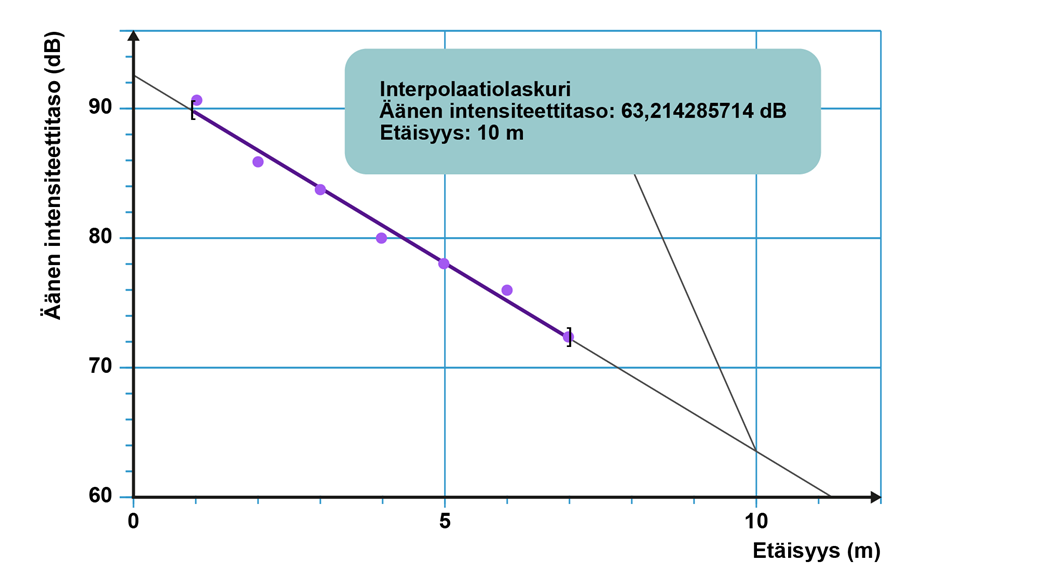
Kuvaajaa ekstrapoloimalla havaitaan, että 10,0 metrin etäisyydellä intensiteettitaso on n. 63 dB.
Kokeellinen tutkimustyö – kävelijän liike
Avaa vähintään 10 metriä pitkä mittanauha suoraksi käytävän lattialle. Ajanottajat asettuvat mitan varrelle metrin välein. Ajanottajien kellot käynnistetään yhtä aikaa ja yksi henkilö kävelee mitattavan matkan. Ajanottajat pysäyttävät kellonsa, kun kävelijä ohittaa heidät. Saadaan kävelyn väliajat yhden metrin välein, ja piirretään näistä kuvaaja aika–paikka-koordinaatistoon. Mittaus voidaan toistaa useammalla eri kävelijällä.
- Palvelun tarjoaa e-Oppi Oy ja Star Cloud OÜ