Keskeisiä kysymyksiä
- Millainen on valosähköinen ilmiö?
- Miksi valosähköisen ilmiön selitys vaatii idean säteilyn kvantittumisesta?
- Miten energian siirtyminen kvantteina ja energian säilyminen ilmenevät valosähköisessä ilmiössä?
Nykyaikaisen luonnontieteen voidaan katsoa alkaneen Galileo Galilein edustamasta tieteellisestä vallankumouksesta 1600-luvulla. Antiikin tieteeseen nähden vallankumouksellista oli kokeellisten menetelmien korostaminen tiedon hankkimisessa. Galilein elinaikana sekä taivaankappaleiden että maanpäällisten kappaleiden liike oli fysiikan tärkein tutkimuskohde. Ennen 1700-lukua Isaac Newton julkaisi mekaniikan lait, jotka kuvasivat edellä mainittujen kappaleiden liikettä. 1700- ja 1800-luvuilla kehittyivät termodynamiikan ja sähkömagnetismin teoriat. Fysiikan mallit aistein havaittavista luonnonilmiöistä olivat varsin kattavia 1900-luvulle tultaessa. Näiden teorioiden kokonaisuutta kutsutaan klassiseksi fysiikaksi.
Jälkeenpäin on todettu 1900-luvun alun edustaneen fysiikan suurta murrosta. Tällöin melko lyhyessä ajassa julkaistiin uusia teorioita liittyen aineen rakenteeseen, säteilyyn sekä ajan ja avaruuden rakenteeseen. Alkaneen modernin fysiikan aikakauden peruspilareiksi kehittyivät kvanttimekaniikka ja suhteellisuusteoria. Nämä teoriat selittivät monia klassisen fysiikan ulottumattomissa olevia aineen ja säteilyn ominaisuuksia. Reilu vuosisata modernin fysiikan kauden alusta sen teknologiset sovellukset, kuten elektroniset laitteet, laserit, lääketieteen kuvantamismenetelmät, ydinvoima ja GPS-paikannusjärjestelmä, ovat läsnä kaikkialla yhteiskunnassamme. Ohessa on ryhmäkuva kvanttifysiikkaa käsitelleen Solvay-konferenssin fyysikoista vuodelta 1927. Heidän joukossaan on monille nykyaikanakin tuttuja fyysikoita.

Resonanssi 7 -oppikirjassa tutkittiin sähkömagneettisen säteilyn ja etenkin valon ilmiöitä. Kirjassa ei kuitenkaan tutustuttu sähkömagneettisen säteilyn ja aineen vuorovaikutukseen täsmällisesti. Sähkömagneettisen säteilyn absorboituessa aineeseen säteily luovuttaa siihen energiaa. Koemme tämän ilmiön, kun auringonvalo lämmittää meitä.
Sähkömagneettisen säteilyn absorptiossa havaitaan kuitenkin piirteitä, jotka poikkeavat aaltoliikkeelle tyypillisestä käyttäytymisestä. Klassinen fysiikka ei pystynyt täsmällisesti selittämään esimerkiksi valon ja metallin vuorovaikutusta, valosähköilmiötä. Tarvittiin uudenlainen teoria kuvailemaan ilmiötä. Valosähköilmiössä säteilyn energia irrottaa elektroneja – "valosähköä" – metallin pinnasta. Ilmiötä demonstroidaan alla olevalla videolla.
Videolla eboniittisauvaan kerääntyy hankauksessa elektronien ylimäärä. Kosketettaessa sinkkilevyä elektroneja siirtyy sauvasta levyyn. Levyyn kiinnitetty elektroskooppi ilmaisee sen varautumisen. Elektronit sitoutuvat metallihilaan tietyn suuruisella energialla, jota kutsutaan irrotustyöksi. On luontevaa olettaa, että valon siirtämä energia voi aiheuttaa elektronien irtoamisen metallista.
Valon aaltomallin kannalta tilannetta voi tarkastella seuraavasti:
Alumiini | 4,28 eV |
Barium | 2,52 eV |
Cesium | 1,94 eV |
Hopea | 4,54 eV |
Kalium | 2,25 eV |
Kalsium | 3,10 eV |
Kulta | 4,83 eV |
Kupari | 4,83 eV |
Litium | 2,46 eV |
Natrium | 2,28 eV |
Nikkeli | 5,09 eV |
Platina | 5,66 eV |
Rauta | 4,63 eV |
Sinkki | 4,34 eV |
Vismutti | 4,22 eV |
Volframi | 4,56 eV |
Elektronit eivät kuitenkaan irtoa näkyvän valon vaikutuksesta pitkänkään ajan kuluessa. Myöskään näkyvän valon kirkkauden eli intensiteetin lisääminen ei muuta tilannetta. Sen sijaan UV-valo irrottaa elektronit ja purkaa varauksen. Havainto paljastaa valon absorptiosta piirteitä, joita on vaikea selittää aaltomallin perusteella.
Ilmiö on selitettävissä seuraavilla seikoilla:
Näiden seikkojen myötä valosähköilmiö tulee ymmärrettäväksi. Näkyvän valon taajuus on sen verran pieni, että valokvanttien energia ei riitä irrottamaan elektroneja, eikä varaus purkaannu levyltä. Intensiteetin lisääminen kasvattaa kvanttien lukumäärää, mutta yksittäisen kvantin energia ei kasva. Sen sijaan UV-valon kvanttien energia riittää elektronien irrottamiseen, jolloin varaus purkautuu.
Yllä esitetyt kvanttimallin postulaatit ovat peräisin Albert Einsteinilta (1879–1955). Hän sovelsi valosähköilmiöön Max Planckin jo aiemmin esittämää hypoteesia säteilyn kvanteista. Einstein julkaisi selityksen ilmiölle vuonna 1905, ja hänelle myönnettiin kyseisen työn nojalla fysiikan Nobelin palkinto vuonna 1921. Valosähköilmiöllä on suuri historiallinen merkitys, koska se edustaa klassisen fysiikan murrosta moderniksi fysiikaksi sekä kvanttifysiikan kauden alkua.
Albert Einstein (1879–1955) oli saksanjuutalainen fyysikko ja eräs tieteen historian myyttisimpiä hahmoja. Hän osoitti kouluaikoina huomattavaa lahjakkuutta matematiikassa ja fysiikassa, mutta ei pitänyt koulun mekaanisesta opetuksesta, mikä johti eroon Münchenin Luitpold-lyseosta seitsemän vuoden opiskelun jälkeen. Einstein päätyi Zürichin Teknilliseen korkeakouluun, josta hän valmistui 1900.
Lopputyönsä jälkeen Einstein onnistui julkaisemaan kapillaari-ilmiötä koskevan tutkimuksen arvostetussa Annalen der Physik -lehdessä. Julkaisut ja hakemukset fyysikoiden assistentiksi eivät kuitenkaan vauhdittaneet Einsteinin tieteellistä uraa. Hän työskenteli valmistumisensa jälkeen opettajana ja patenttivirkailijana. Näiden toimiensa ohella Einstein tutki fysiikkaa ja sai aikaan neljä hyvin merkittävää työtä. Työt koskivat valosähköistä ilmiötä, suhteellisuusteoriaa ja Brownin liikettä. Kaikki työt valmistuivat vuonna 1905, joka tunnetaan fysiikan historiassa annus mirabiliksena, ihmeiden vuotena.
Einsteinin töiden merkitys oli valtaisa modernin fysiikan kehitykselle. Valosähköilmiön selitys toimi kvanttifysiikan perustana, ja suhteellisuusteoria oli täysin uudentyyppinen Newtonin mekaniikkaa tarkentava teoria. Einsteinin ehkäpä suurin saavutus oli kuitenkin yleinen suhteellisuusteoria. Se on erityisen suhteellisuusteorian laajennus, joka selitti gravitaatiovuorovaikutuksen uudella tavalla, aika-avaruuden kaareutumisena. Sen ennustamat gravitaatioaallot havaittiin kokeellisesti vuonna 2016 LIGO-havaintolaitteella. Yleinen suhteellisuusteoria on nykyfysiikan toinen perusteoria hiukkasfysiikan standardimallin kanssa. Nämä yhdistämällä pyritään saavuttamaan "kaiken teoria", mikä oli myös Einsteinin tavoite hänen viimeisten 30 elinvuotensa aikana. Einstein kuoli v. 1955 Yhdysvalloissa, jonne hän muutti lukuisten muiden saksalaisten tiedemiesten tavoin natsihallintoa pakoon.

Tarkastellaan valosähköilmiötä edellä esitetyn kvanttihypoteesin ja energian säilymislain näkökulmasta. Säteily luovuttaa metallille energiaa yksittäisinä kvantteina. Jos taajuus on pieni, kvanttien energia on niin pieni, että niiden energia ei voi irrottaa elektroneja. Säteilyn taajuuden suurentaminen kasvattaa kvanttien energiaa, kunnes kvanttien energia mahdollistaa elektronien irrottamisen.
Rajataajuus, jolla elektroneja alkaa irrota, on jokaiselle metallille eri suuruinen. Rajataajuudella kvanttien energia on yhtä suuri kuin metallille ominainen irrotustyö,
Kuvasarjassa on eri taajuisen säteilyn ja aineen välinen vuorovaikutus.
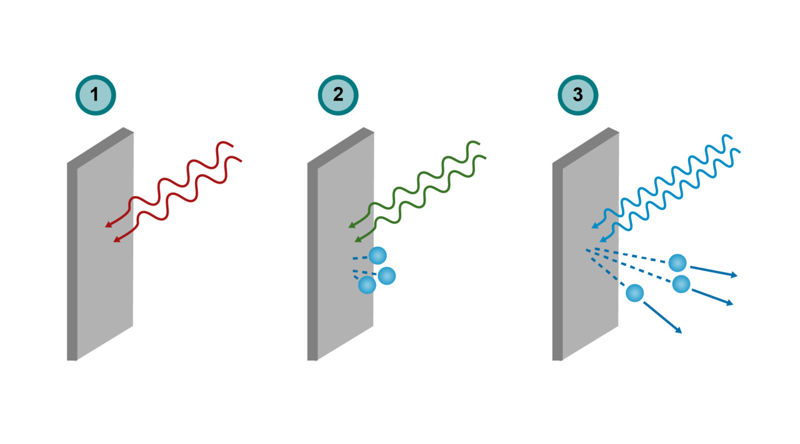
Sähkömagneettisen säteilyn energia esiintyy paketteina, joita kutsutaan kvanteiksi. Säteily absorboituu tai emittoituu yksi kvantti kerrallaan. Kvantin energiasta riippuu, tapahtuuko valosähköilmiö.
Energian säilyminen valosähköilmiössä voidaan ilmaista seuraavalla yhtälöllä:
Kvantin energia muuntuu irrotustyöksi ja elektronien liike-energiaksi. Yllä oleva yhtälö kirjoitetaan usein muodossa, jossa elekroneille jäävä liike-energia lasketaan kvantin energian ja irrotustyön erotuksena.
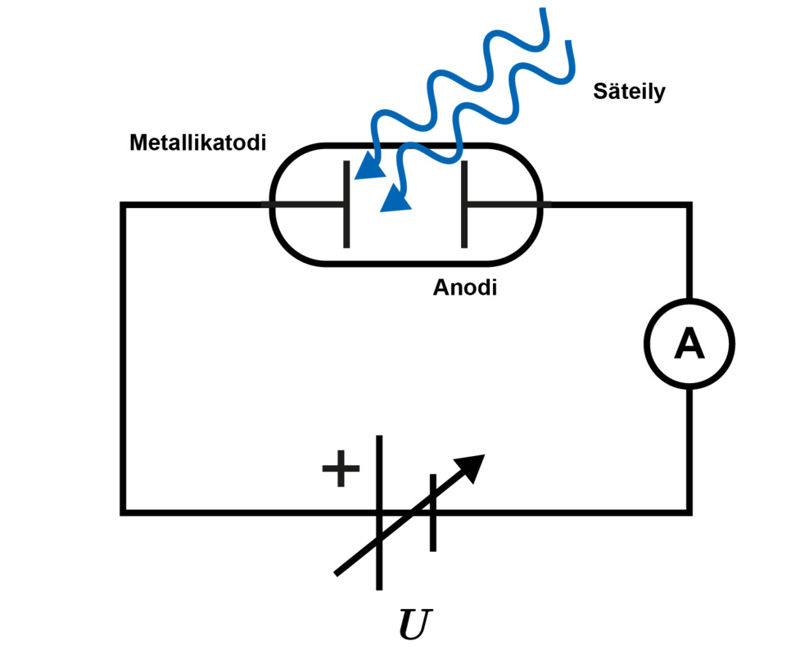
Yllä esitetyn yhtälön todentaminen on mahdollista mittalaitteistolla, jossa metallilevyyn kohdistetaan valoa ja irtoavien elektronien energia voidaan määrittää. Tähän soveltuva kytkentä on esitetty oheisessa kuvassa.
Katodi ja anodi on sijoitettu tyhjiöputkeen ja irtoavat elektronit synnyttävät sähkövirran virtapiiriin. Sähkövirta saadaan lakkaamaan kytkemällä virtapiiriin anodin ja katodin välille pysäytysjännite U, jonka tuottama sähköinen voima vastustaa katodista irronneiden elektronien liikettä. Tällöin sähkökenttä tekee työtä elektronien liikkeen pysäyttämiseksi.
Sähkökentän tekemä työ:
Tutkimuksessa pysäytysjännite säädetään sellaiseksi, että sähkövirta piirissä lakkaa.
Tutkitaan kvanttien energian riippuvuutta säteilyn taajuudesta. Kohdistetaan katodiin säteilyä eri taajuuksilla ja määritetään irtoavien elektronien suurin liike-energia. Kun rajataajuus on ylitetty, elektronien liike-energian havaitaan kasvavan taajuuden suurentuessa. Liike-energian suuruus saadaan selville, kun elektronien virta juuri ja juuri lakkaa. Tällöin sähkökentän tekemä työ on yhtä suuri kuin elektronien liike-energia
Pysäytysjännitteen ollessa
Energian perusyksikkö joule (J) on varsin suuri yksikkö säteilykvanttien energioihin nähden. Usein on käytännöllisempää käyttää energian yksikköä, elektronivolttia. Kun elektroni kiihdytetään sähkökentässä, jonka jännite on 1 V, sähkökentän tekemän työn kautta saadaan energian suuruudeksi
Joulen ja elektronivoltin välinen muuntokerroin on alkeisvarauksen lukuarvo coulombeissa, ts. niiden välillä pätee seuraava yhtälö:
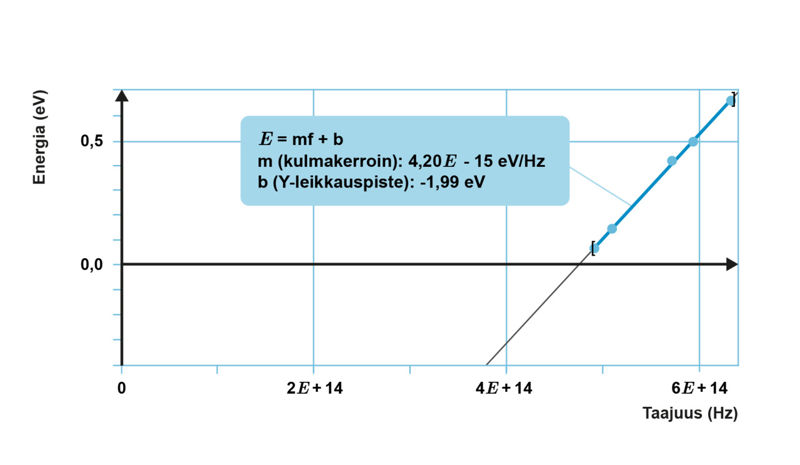
Erästä metallia tutkittaessa havaittiin elektronien suurimman liike-energian ja valon taajuuden välillä oheisen kuvaajan mukainen riippuvuus.
Pisteet asettuvat suoralle. Kvantin energia kasvaa lineaarisesti taajuuden suurentuessa. Ilmiötä kuvaa matemaattinen lauseke:
Kulmakerrointa kutsutaan Planckin vakioksi
Säteilykvantin energian yksikkö on joko joule tai elektronivoltti. Energian yksikkö määräytyy sen mukaan, kumpaa yksikköä Planckin vakiolle käytetään.
Säteilykvantin energia on Planckin vakion
Aaltoliikkeen perusyhtälön mukaan
Suoran yhtälössä
Kaavassa taajuus
Valosähköilmiössä sähkömagneettisen säteilyn kvantti luovuttaa energiansa metallin elektronille. Osa energiasta kuluu irrotustyöhön
Huomaa, että tämä kaava tulee perustella energiaperiaatteen näkökulmasta aina kaavaa käytettäessä.

1. Sähkömagneettisen säteilyn kvantin energia ei riitä irrottamaan elektronia metallilevyltä. Mitä pitäisi tehdä?
2. Sähkömagneettisen säteilyn taajuus on sama kuin erään metallin rajataajuus.
Negatiivisesti sähkövarattuun sinkkilevyyn kohdistetaan ensin näkyvää valoa ja sen jälkeen ultraviolettivaloa. Näkyvä valo ei vaikuta levyn varaukseen, mutta uv-valon vaikutuksesta varaus purkautuu.
a. Elektronin irtoaminen metallista vaatii metallille ominaisen määrän, irrotustyön, verran energiaa. Valon energia absorboituu metalliin yksi kvantti kerrallaan. Kvantin energia on suoraan verrannollinen valon taajuuteen:
b. Intensiteetin kasvattaminen ei muuta yksittäisen kvantin energiaa, joka riippuu vain valon taajuudesta. Näkyvän valon kvantin energia ei riitä purkamaan sähkövarausta, joten intensiteetin kasvattaminen ei muuta tilannetta.
Metalliin kohdistettiin valoa, jonka taajuutta muuteltiin. Valon irrottamien elektronien suurimmat liike-energiat määritettiin. Liike-energian riippuvuutta säteilyn taajuudesta mallinnettiin ohessa esitetyllä suoralla.
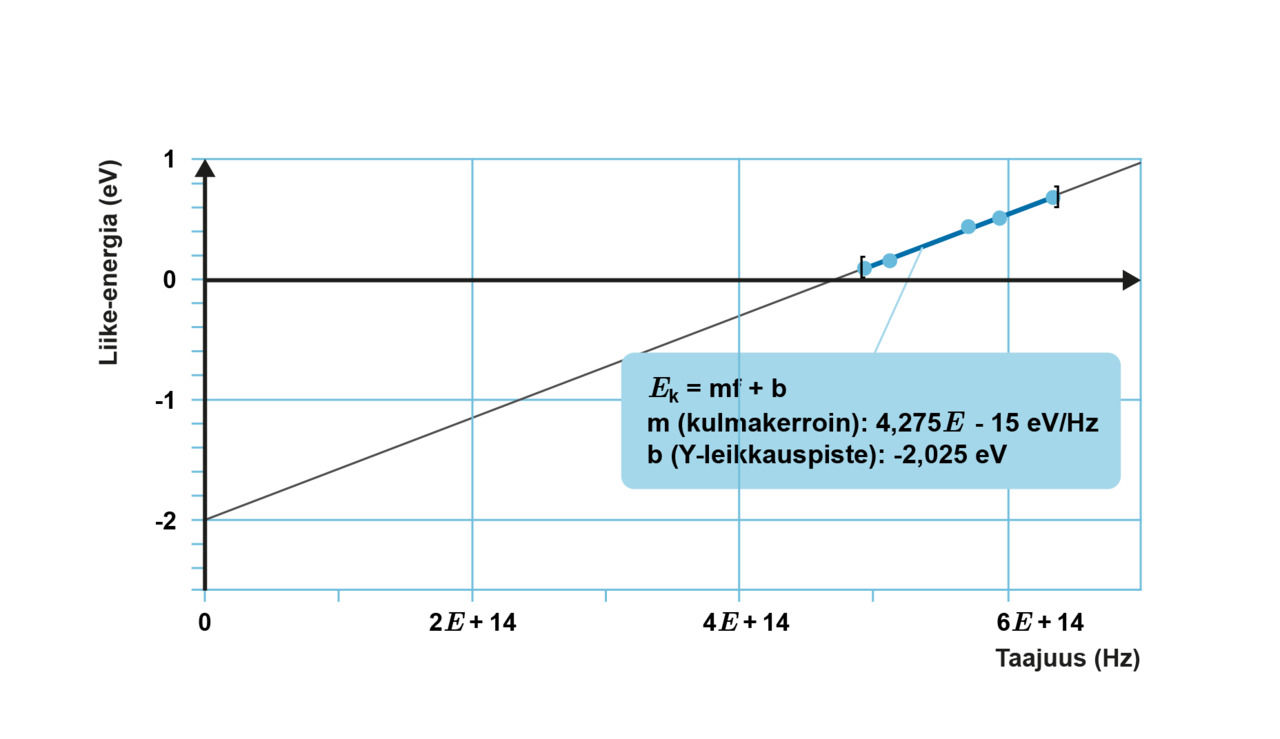
a. Valosähköilmiössä energian säilymisestä seuraa, että metalliin absorboituvan fotonin energia muuttuu irrotustyöksi ja irronneen elektronin liike-energiaksi. Tätä kuvataan seuraavalla yhtälöllä:
Kun tähän yhdistetään tieto säteilykvantin energiasta
b. Planckin vakio on suoran kulmakerroin. Mallin parametrien perusteella
Kohta, jossa suora leikkaa pystyakselin, on irrotustyön vastaluku. Mallin parametrien perusteella
Metalli voisi olla cesiumia, sillä irrotustyö on lähellä sen taulukkoarvoa.
Laserin valon aallonpituus on 514 nm.
a. Fotonin energia voidaan laskea yhtälöstä
Energia on elektronivolteissa 2,41 eV ja jouleissa 3,86 ⋅ 10-19 J.
b. Merkitään liike-energia yhtä suureksi kuin fotonin energia ja ratkaistaan nopeus. Laskussa pitää käyttää fotonin energialle yksikköä joule, koska se on liike-energialle nopeuden ja massan perusyksiköistä muodostuva johdannaisyksikkö.
Nopeus on 920 km/s.
Valo, jonka aallonpituus on 614 nm, osuu valokennoon. Tällöin tarvitaan 0,29 V:n pysäytysjännite estämään katodilta irronneiden elektronien pääsy anodille. Kuinka suuri pysäytysjännite tarvitaan, jos valon aallonpituus on 468 nm?
Valosähköilmiössä metalliin absorboituvan fotonin energia muuttuu irrotustyöksi ja irronneen elektronin liike-energiaksi:
Fotonin energia voidaan ilmaista aallonpituuden avulla. Sähkökenttä tekee työn
Voidaan ratkaista irrotustyö:
Energian säilymisyhtälöä voidaan nyt soveltaa uudestaan tilanteeseen, jossa aallonpituus on 468 nm. Ratkaistaan kentän tekemä työ
Kentän pitää tehdä 0,92 eV:n työ, joten tarvitaan 0,92 voltin jännite.
1. Mitä tapahtuu, kun valon intensiteettiä kasvatetaan?
2. Mitä tapahtuu, kun metalliin osuva valo vaihdetaan aallonpituudeltaan lyhyemmäksi?
3. Metalli vaihdetaan alumiiniin. Alumiinin irrotustyö on 4,28 eV. Irtoaako alumiinista elektroneja, kun ledin 590 nm:n valo kohdistetaan sen pintaan?
4. Kuinka suuri on korkeintaan aallonpituus sellaiselle valolle, joka aiheuttaa valosähköilmiön alumiinissa?
nm
5. Mikä valosähköilmiössä osoittaa säteilyn energian kvantittumisen?

1. Radioaaltojen taajuus on 104 MHz. Laske radioaaltojen aallonpituus.
m
2. Näkyvän valon fotonin aallonpituus on 555 nm. Laske fotonin taajuus.
THz
3. Fotonin taajuus on 23 ⋅ 1013 Hz. Laske fotonin energia jouleissa.
⋅ 10−19 J
4. Fotonin energia on 7,2 ⋅ 10−13 J. Laske fotonin energia yksikössä eV.
MeV
5. Fotonin aallonpituus on 624 nm. Laske fotonin energia yksikössä eV.
eV

Mitä haluat tehdä tekstillä? Teksti käsitellään tekoälyn avulla, eikä sitä sen jälkeen muokata tai tarkisteta. Tekstissä voi esiintyä virheitä. Tarkista tekstin oikeellisuus vertaamalla sitä kirjan alkuperäistekstiin.
Valitse tiedostot, jotka haluat lisätä. Tuetut formaatit ovat txt, html, htm, pdf, odt, odp, ods, xls, xlsx, ppt, pptx, pps, doc, docx, rtf, png, jpg, jpeg ja gif.
| Nimi | |
|---|---|
| poista |
Huom.! Linkkien tulee alkaa ”http://”!
Opiq käyttää verkkosivun toiminnan, turvallisen käytön varmistamisen, käytön analysoimisen ja parhaan käyttömukavuuden tarjoamisen edellyttämiä evästeitä.
Eväste on käyttäjän tietokoneelta verkkosivun palvelimeen lähetettävä pieni tiedosto, joka sisältää verkkosivun toiminnan edellyttämiä käyttäjää ja hänen tekemiä valintoja koskevia tietoja.
Isoin osa evästeistä ovat Opiqin toiminnan kannalta välttämättömiä. Analyyttisistä evästeistä voi luopua ja silloin ei sinun käyttötietojasi ei käytetä Opiqin kehittämiseen. Lue lisää