Keskeisiä kysymyksiä
- Missä tilanteissa kappale kiertyy?
- Miten määräytyy voiman vääntövaikutuksen eli momentin suuruus?
- Miten voiman suunta vaikuttaa vääntövaikutuksen suuruuteen?
Renkaan pultin avaamiseen voidaan käyttää momenttiavainta. Pulttiin kohdistuu voiman vääntövaikutus, joka kiertää pultin auki. Momenttiavaimen pitkä varsi kasvattaa vääntövaikutusta, jolloin pultin avaaminen onnistuu kohtuullisen vähäisellä voimalla.
Pulttia vääntävä voima ei siirrä pulttia, vaan muuttaa sen asentoa, jolloin pultti kiertyy. Voiman vääntövaikutusta kuvaava suure on momentti. Oppikirjassa Resonanssi 4 tutkittiin tilanteita, joissa voimilla ei ollut vääntövaikutusta, tai se oli merkityksetöntä. Vääntövaikutus otetaan huomioon tilanteissa, joissa kappaleen kiertyminen on sekä mahdollista että kiinnostavaa.

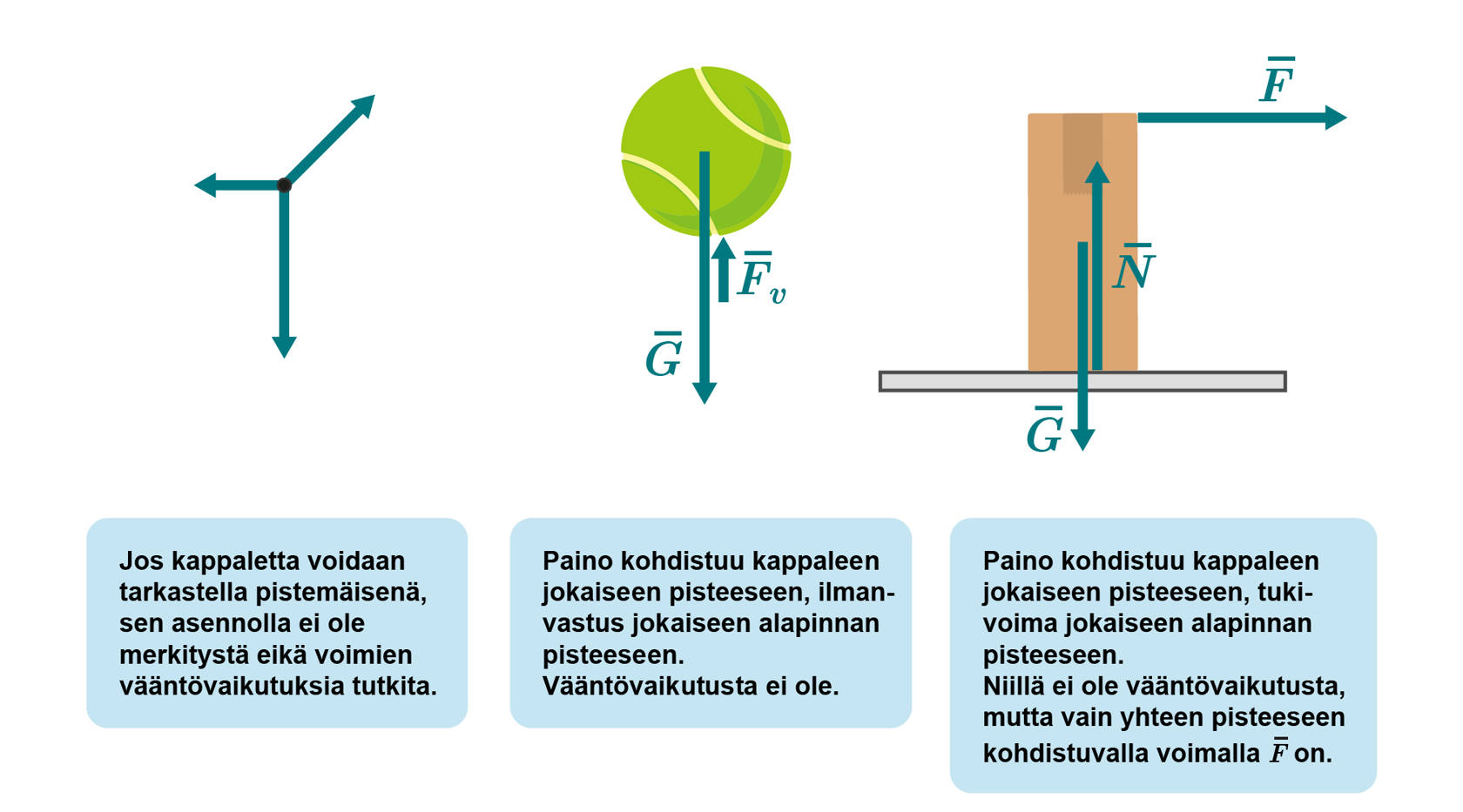
Voiman vääntövaikutus korostuu, kun voima kohdistuu kappaleeseen epäsymmetrisesti. Tasaisesti kappaleen pintaan kohdistuva voima, esimerkiksi koko pallon alapintaan kohdistuva ilmanvastus, ei aiheuta vääntövaikutusta. Voima pyrkii siirtämään kappaleen jokaista pistettä ja saa siten pallon putoamaan samassa asennossa. Sen sijaan vain kappaleen yläreunaan kohdistuva voima aiheuttaa vääntövaikutuksen ja voi vääntää kappaleen nurin.

Kappaletta on haastavaa pitää tasapainossa vain yhteen pisteeseen kohdistuvalla tukivoimalla. Kappaleesta, kuten kynästä, tartutaan useasta kohtaa tukipisteiden lisäämiseksi.
Kappaleen tasapainottaminen vain yhdellä tukivoimalla on kuitenkin mahdollista. Moni lienee kokeillut kynän pitämistä tasapainossa yhdellä sormella, ja joskus luontokin luo eriskummallisia rakennelmia.
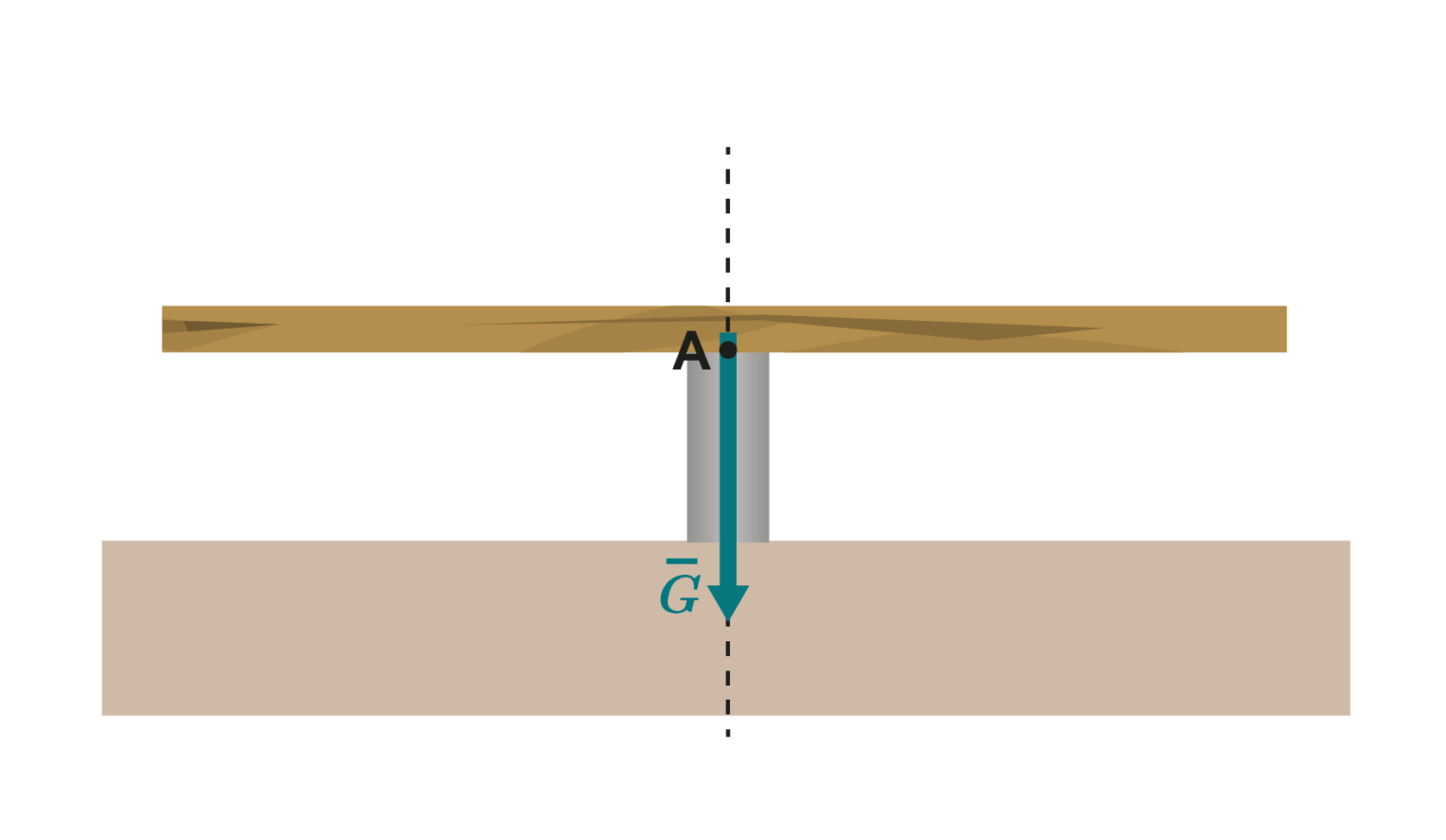
Yksittäinen tukipiste pitää kappaleen tasapainossa vain, jos painon vaikutussuunta kulkee tuetun alueen läpi. Tällöin tukivoimalla ja painolla ei ole vääntövaikutuksia. Kuvassa rima pysyy tasapainossa, koska painon vaikutussuunta (merkitty katkoviivalla) kulkee tukipisteen A kautta.

Symmetrisissä ja tasa-aineisissa eli homogeenisissa kappaleissa kappaleen painopiste on sen keskipisteessä. Vaikka kappaleilla on muoto, kappaleet voidaan useissa tilanteissa yksinkertaistaa pistemäisiksi. Tällöin tilannekuvissa kappaleet piirretään symmetrisiksi ja painopiste sijoitetaan kappaleen keskelle.
Kun tukipiste ei ole painopisteen vaikutussuoralla, yksittäinen tukipiste ei pysty kumoamaan painon vääntövaikutusta. Alla olevassa valokuvassa rima on tuettu yhdestä päästä statiivitankoon. Sen alla on havainnekuva voimista, joilla on vääntövaikutus kiinnityspisteen suhteen. Rima pysyy tasapainossa, koska sitä tuetaan myös toisesta päästä. Jos tuki irrotetaan, rima kääntyy.

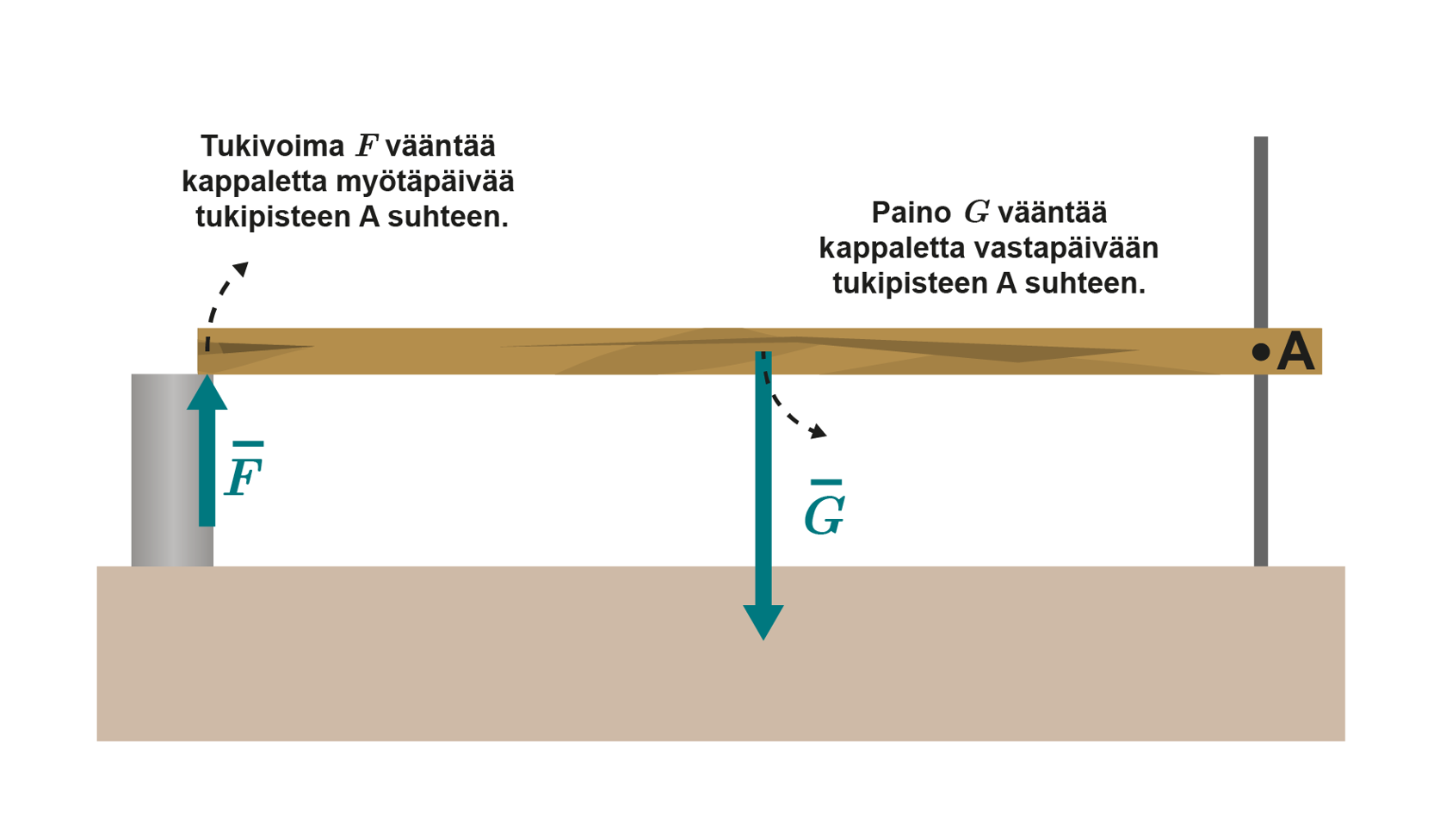
Tutkitaan voiman vääntövaikutuksen suuruutta edellisen tilanteen viivaimessa. Viivaimen paino kohdistuu viivaimen painopisteeseen, keskelle viivainta ja tukivoimat viivaimen päihin tuettujen pisteiden alueelle. Jotta painon vääntövaikutus tukipisteen A suhteen saadaan kumottua, tarvitaan toinen tukivoima. Viivain pysyy tasapainossa, kun voimien vääntövaikutukset eli momentit kumoavat toisensa. Jos momentit eivät kumoa toisiaan, viivain kiertyy akselin A ympäri.
Mitataan tukivoiman suuruus voima-anturilla, ja luetaan viivaimelta voiman vaikutuspisteen etäisyys kiertoakselista A. Mittaus on tehty oheisella videolla, ja tulokset on sijoitettu -koordinaatistoon.
Alla ovat videon mittauksesta saadut tulokset ja kuvaaja. Koordinaatiston pistejoukkoon sopii erinomaisesti funktio, jossa .
0,13 | 23,36 | 3,0 |
0,17 | 17,17 | 2,9 |
0,27 | 11,07 | 3,0 |
0,37 | 7,84 | 2,9 |
0,47 | 6,19 | 2,9 |
0,57 | 5,00 | 2,9 |
0,67 | 4,28 | 2,9 |
0,77 | 3,74 | 2,9 |
0,87 | 3,29 | 2,9 |
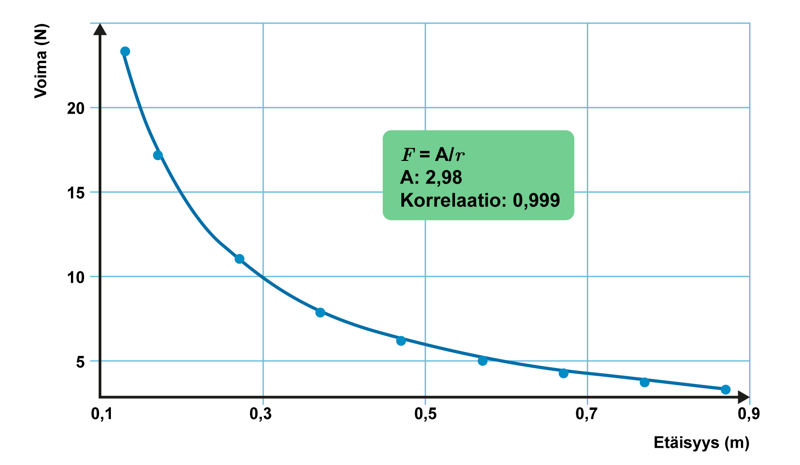
Tukivoiman suuruus on kääntäen verrannollinen etäisyyteen. Mitä suurempi tukipisteen etäisyys kiertoakselista on, sitä pienempi on kannattelemiseen tarvittava voima. Voiman ja etäisyyden tulo pysyy vakiona ja kuvaa siten tangon paikallaan pitämiseksi vaadittua vääntövaikutusta. Tätä ilmentävä suure on momentti.
Momentin etumerkki kertoo vääntövaikutuksen kiertosuunnan. Painon ja tukivoiman aiheuttamat momentit ovat yhtä suuret, mutta vastakkaismerkkiset, joten niiden vääntövaikutukset kumoavat toisensa, ja viivain pysyy paikallaan.
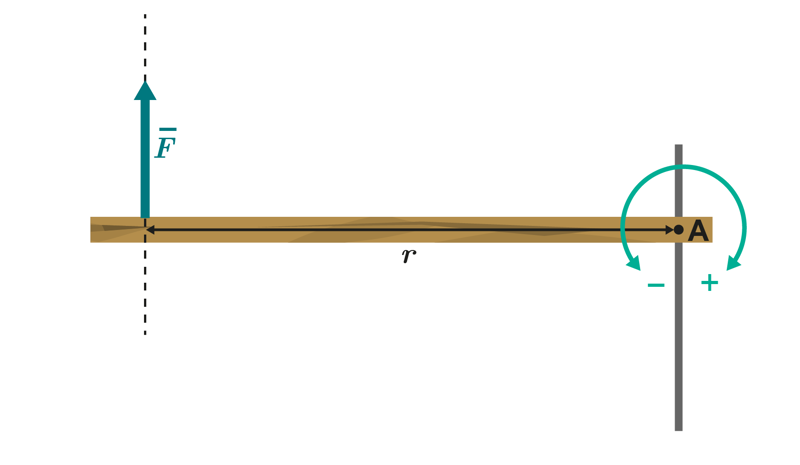
Voiman momentti eli vääntövaikutus on voiman ja kiertoakselin ja voiman välisen vaikutussuoran kohtisuoran etäisyyden tulo.
Kiertoakselin ja voiman vaikutussuoran välistä etäisyyttä voidaan kutsua myös voiman varreksi.
Momentin yksiköksi tulee newtonmetri:
Kuvioon merkitään kaarinuolella, kumpi kiertovaikutuksen suunta on positiivinen, tai merkkivalinta kerrotaan sanallisesti.

Huomioitavaa on, että matkan ja voiman tulo voi kuvata työtä tai momenttia . Energia on skalaarisuure, jonka yksikkö on joule, ja momentti on vektorisuure, jonka yksikkö on newtonmetri. Ne ovat siis eri suureita, eikä niitä tule sekoittaa.
Voiman vääntövaikutus lasketaan voiman vaikutussuunnan lyhimmästä etäisyydestä kiertoakseliin. Edellä tarkastelluissa tilanteissa voima ja sen etäisyys kiertoakselista olivat toisiinsa nähden kohtisuorassa. Etäisyys on pienin, kun se on kohtisuorassa voimaan nähden. Jos viivainta tasapainottava voima on vino, lyhin etäisyys ei ole viivaimen pituus, vaan kohtisuora etäisyys voiman vaikutussuorasta kiertoakseliin.
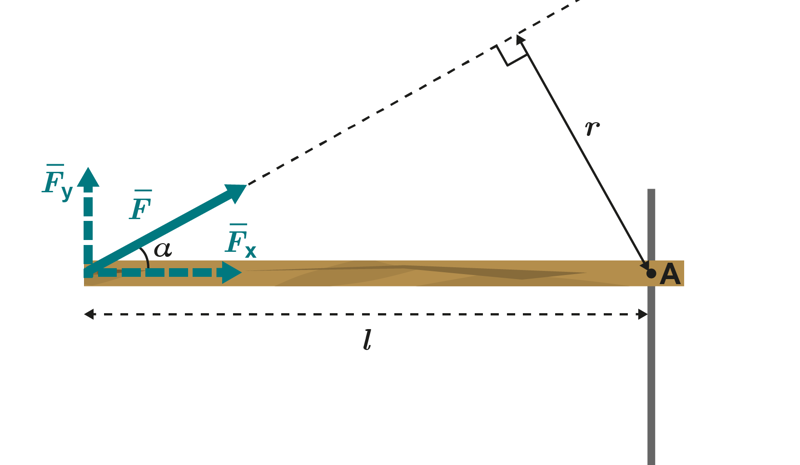
Voiman momentin suuruudelle pätee lauseke
.
Tilanne voidaan ajatella myös siten, että viivainta kannattelee vain voiman pystysuora komponentti . Viivaimen suuntainen voiman komponentti pyrkii työntämään viivainta kohti kiertoakselia, eikä käännä viivainta akselin ympäri. Momentin suuruudelle saadaan täten toinen muoto.
Momenttien suuruudet ovat samat riippumatta lausekkeen muodostamistavasta. Etäisyys on osa suorakulmaista kolmiota, jonka hypotenuusa on . Voiman ja viivaimen välisen kulman α avulla saadaan ehto , joten momentin suuruus on
.
Toisaalta voiman komponentti on voiman avulla ilmoitettuna
.
Kun tämä sijoitetaan momentin lausekkeeseen, saadaan
.
Usein voiman jakaminen komponentteihin on helpoin tapa laskea momentin suuruus, mutta jokaista tilannetta kannattaa tarkastella tapauskohtaisesti. Tunnetut lähtöarvot määrittävät, mikä on yksinkertaisin tapa laskea momentin suuruus.
1. Tanko pysyy paikallaan, kun punnus on kuvan osoittamassa paikassa. Mitä tapahtuu, kun punnusta siirretään oikealle?
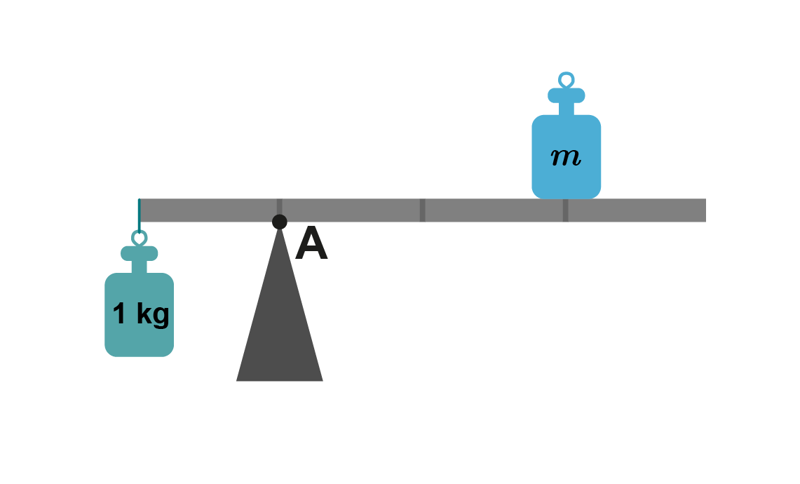
2. Kuinka suuri on massa , jos tangon massa oletetaan hyvin pieneksi?
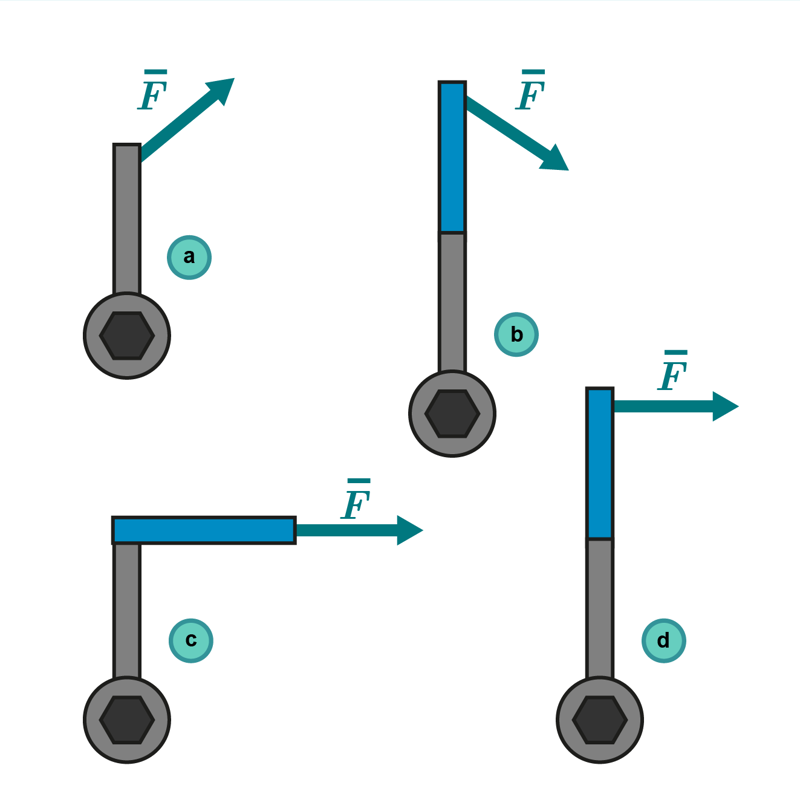
3. Juuttunutta mutteria avataan jatkettavalla jakoavaimella. Millä tavalla mutteri aukeaa varmimmin? Voiman suuruus on sama joka tilanteessa.
Tankoa kannatellaan tasapainossa sen toisesta päästä (Kuva A). Kannattelevan voiman suuruus on 76 N. Tangon pituus on 135 cm.
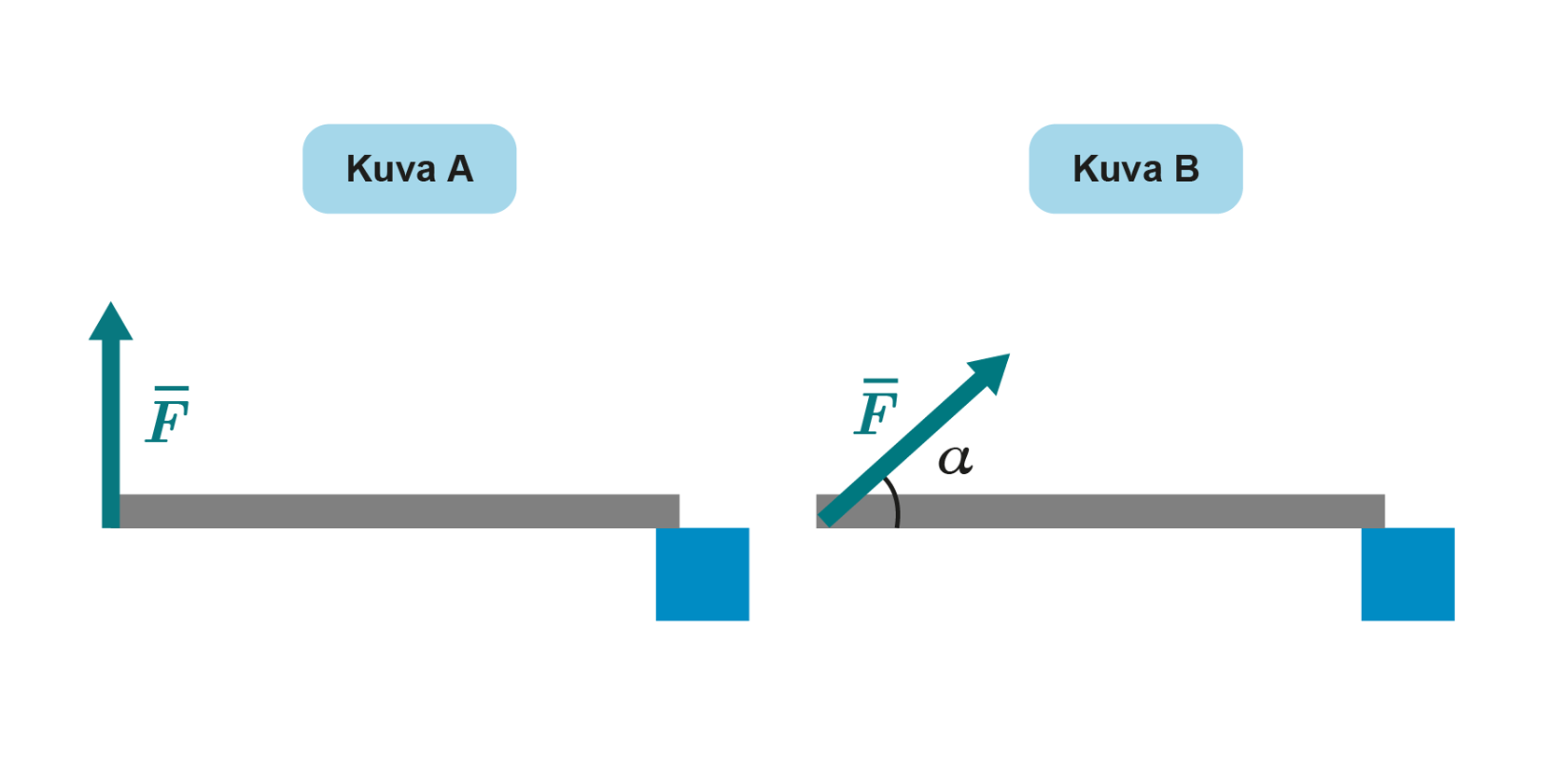
a. Voiman momentti saadaan laskettua:
Tanko on tasapainossa. Painon momentti on yhtä suuri, mutta vaikuttaa vastakkaiseen suuntaan kuin voiman momentti. Painon momentti on 100 Nm.
b. Jotta tanko pysyy tasapainossa, kannattelevan voiman momentin on oltava yhtä suuri kuin painon momentti. Painon momentti ei muutu, joten myös kannattelevan voiman momentti on yhä sama kuin a-kohdassa.
Kun kannattelupistettä siirretään kohti tangon keskipistettä, kannattelevan voiman varsi lyhenee.
Koska momentti ei muutu ja voiman varsi lyhenee, kannatteleva voima suurenee.
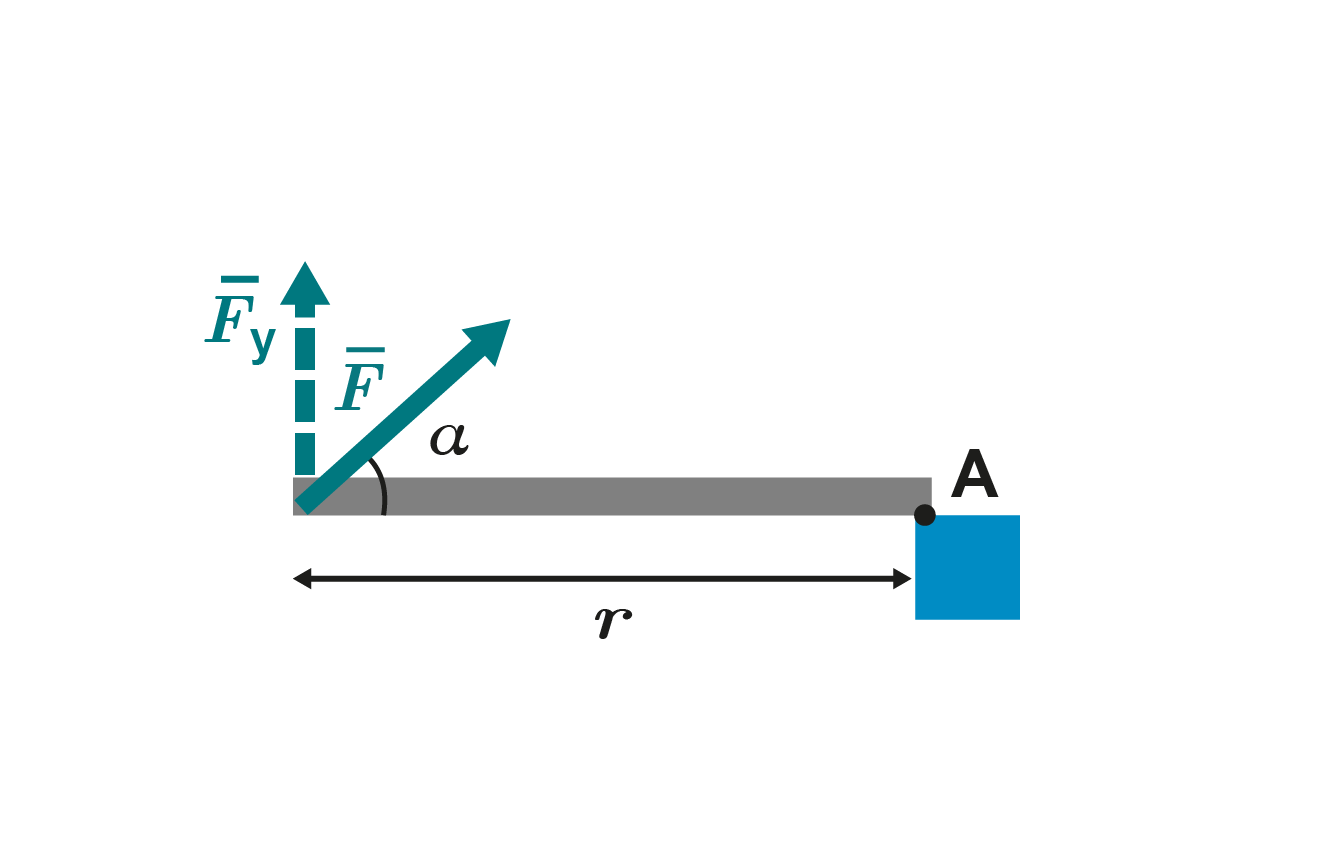
c. Kannattelevan momentin suuruus lasketaan toisiinsa nähden kohtisuorassa olevien voiman ja etäisyyden tulona.
Ilmoitetaan komponentti voiman avulla.
Lausekkeessa saa arvoja välillä 0–1. Se on sitä pienempi, mitä pienempi on kulma. Voima on tällöin sitä suurempi, mitä pienempi on kulma . Kannatteleva voima on pienin, kun se on suoraan ylöspäin.
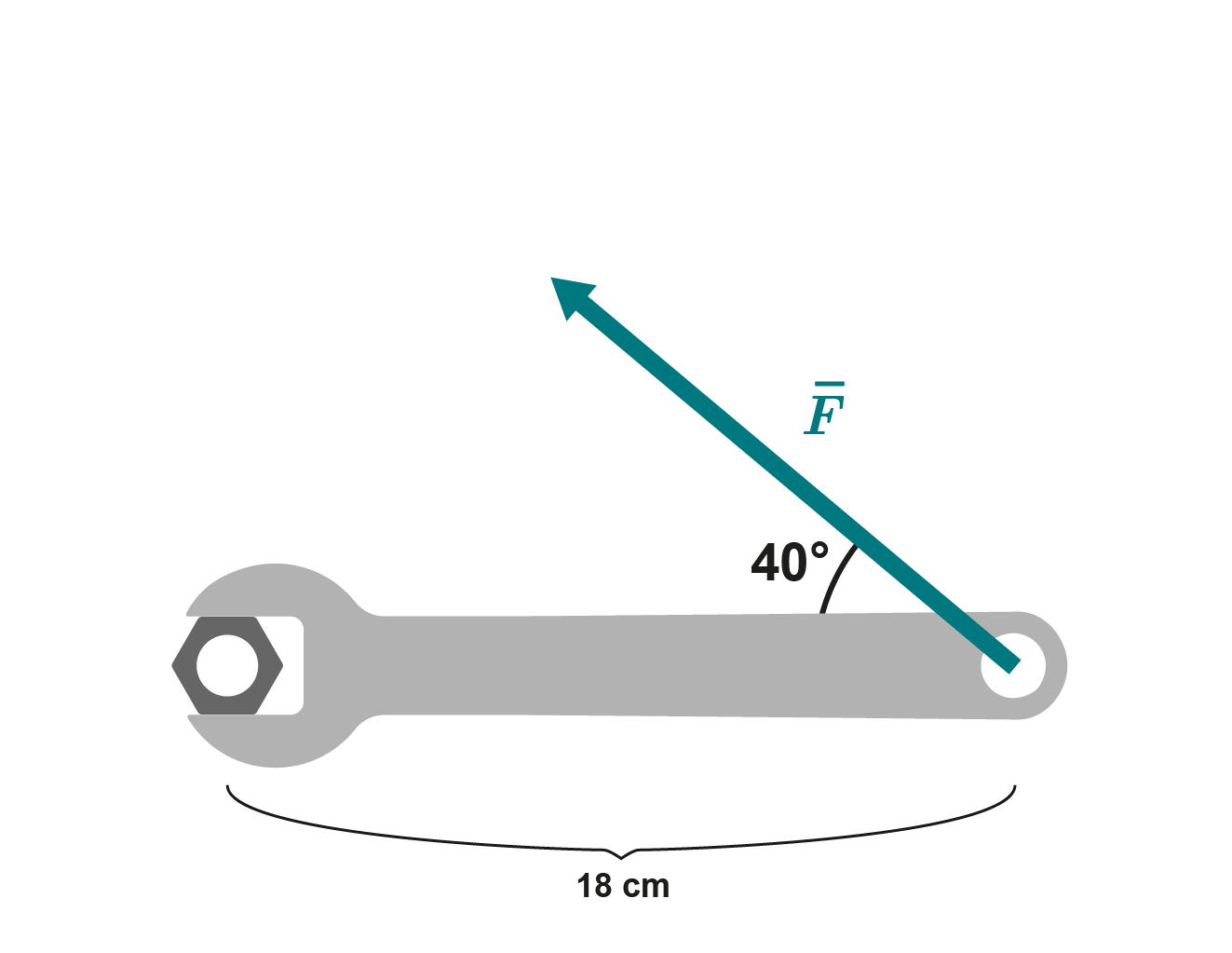
Joskus joudutaan työskentelemään ahtaissa ja hankalissa tiloissa. Tiedetään, että erään mutterin avaamiseen vaaditaan 58 Nm:n momentti.
Nyt on käytettävissä jakoavain, joka on 18 cm pitkä ja jota voidaan työntää jyrkimmillään 40 asteen kulmassa.
Laske voima, joka jakoavaimeen pitää kohdistaa mutterin avaamiseksi.
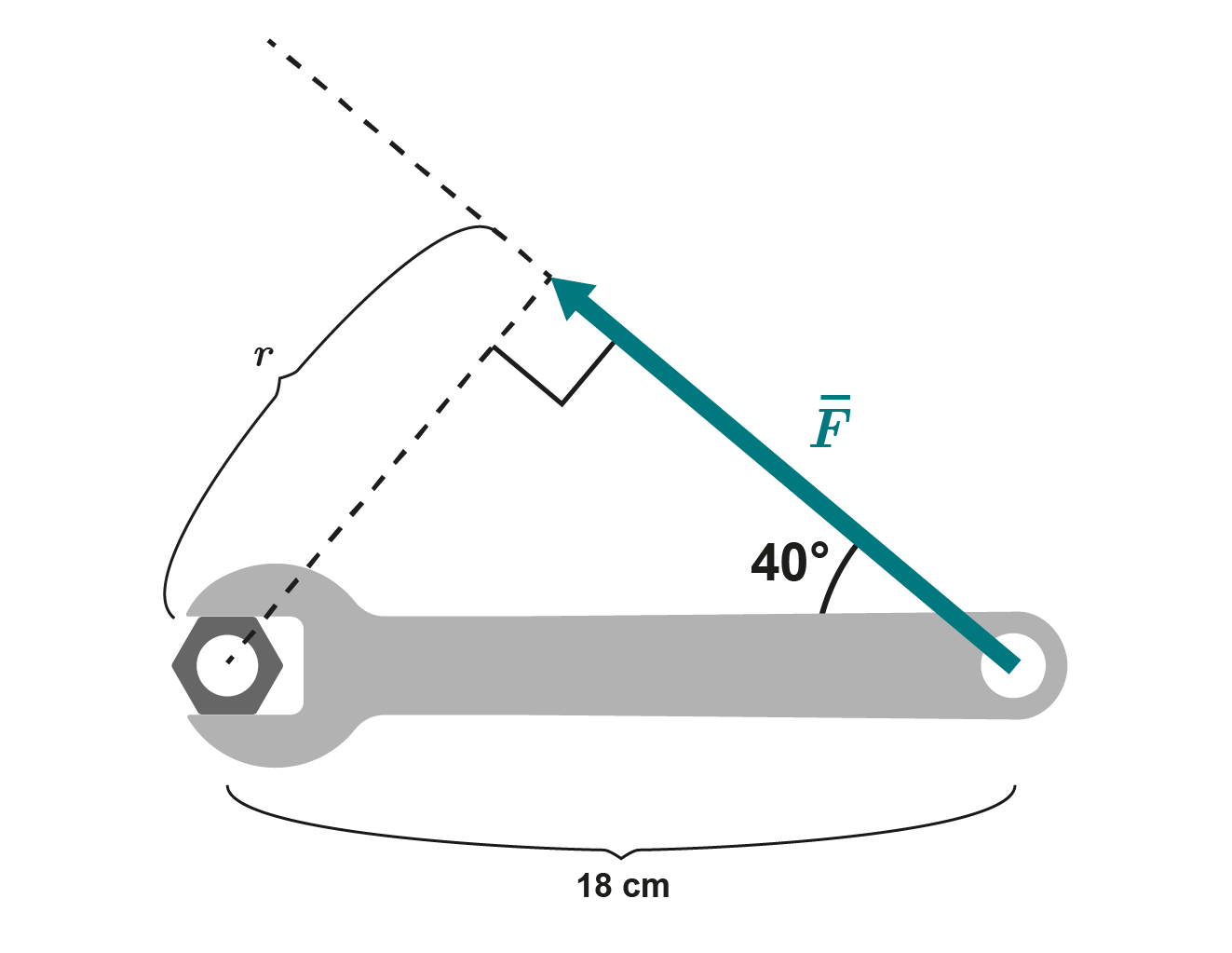
Täydennetään havainnollistavaa kuvaa momentin laskemiseksi. Muodostuvasta kolmiosta voidaan laskea voiman vaikutussuoran etäisyys pyörimisakselista eli voiman varsi.
Trigonometrialla saadaan
Nyt voidaan käyttää momentin määritelmää ja ratkaista vaadittu voima:
Jakoavaimeen pitää kohdistaa noin 500 newtonin voima.
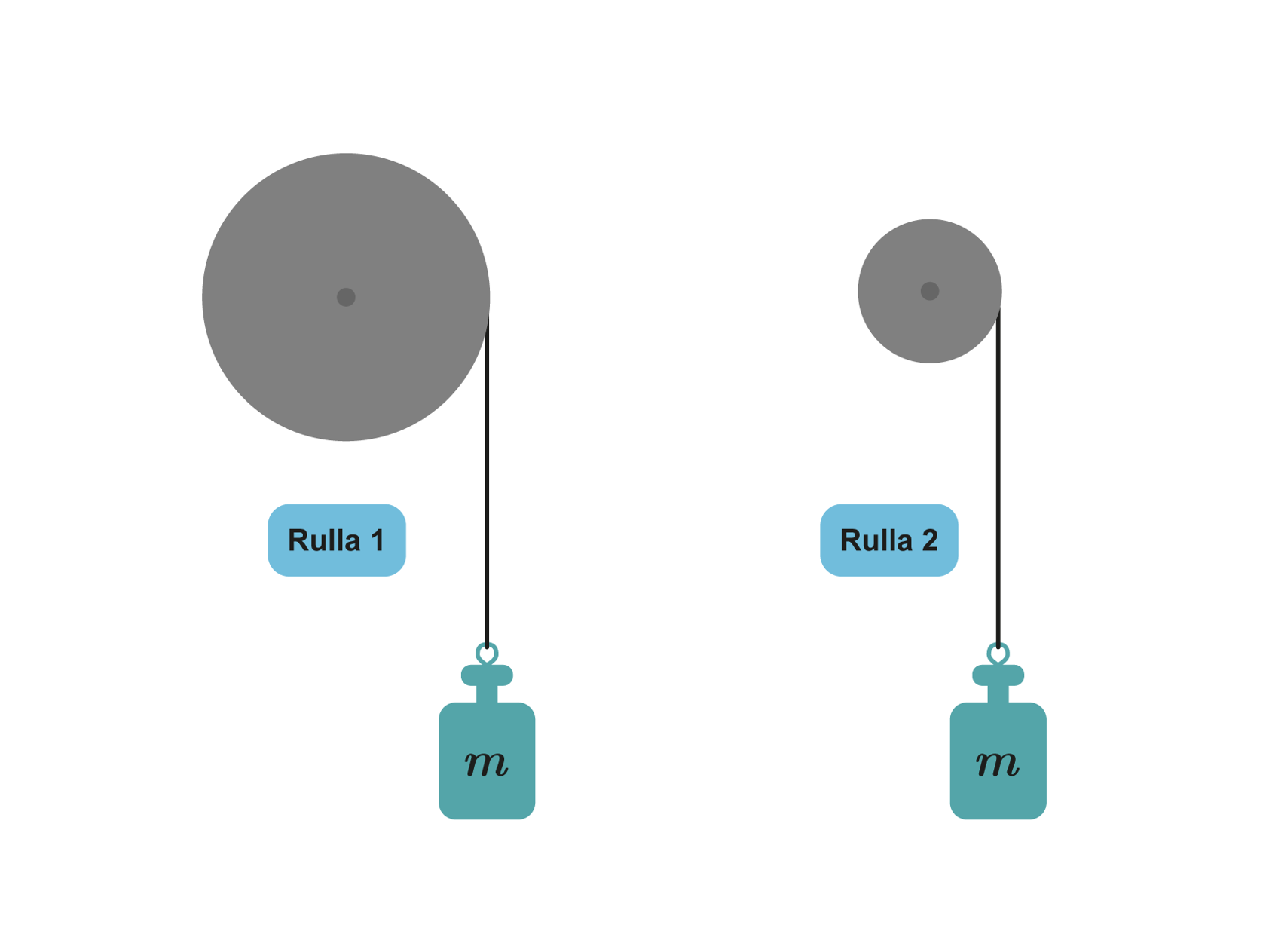
1. Punnus, jonka massa on , on kiinnitetty langalla keskeltä akseloituun rullaan. Kumpi rullista on vaikeampi pitää paikallaan pyörimättömänä?
2. Rullan 1 halkaisija on kaksinkertainen rullan 2 halkaisijaan verrattuna. Kumpi rullista on vaikeampi pitää paikallaan pyörimättömänä, kun rullaan 2 lisätään toinen samanlainen punnus?
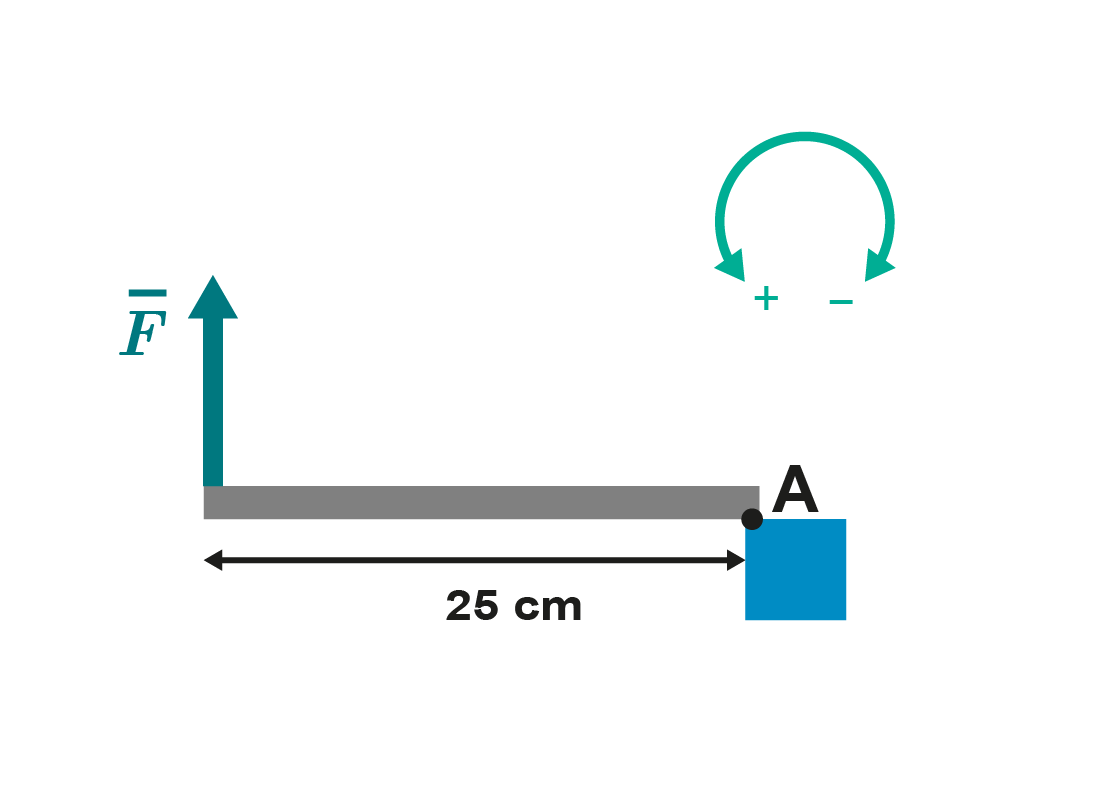
3. Voiman suuruus on 10 N. Kuinka suuri on voiman momentti kiertoakselin A suhteen? Ilmoita vastaus kahden merkitsevän numeron tarkkuudella. Huomioi momentin merkki.
Nm
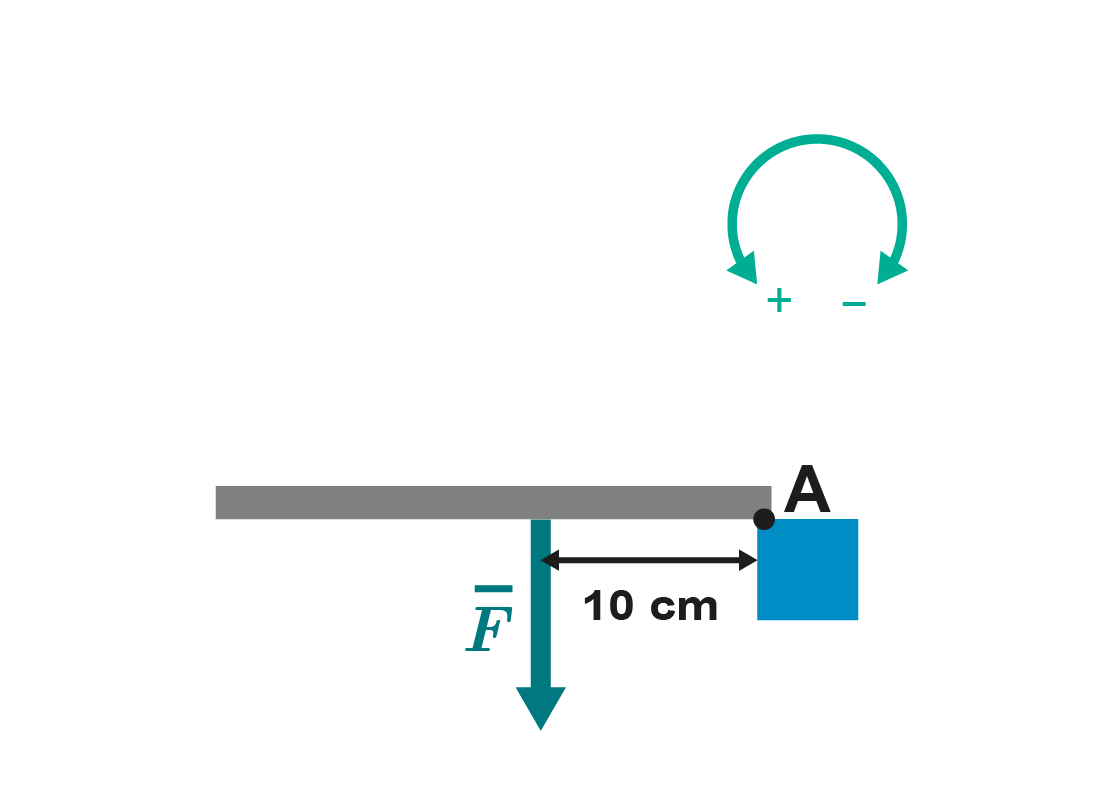
4. Voiman suuruus on 10 N. Kuinka suuri on voiman momentti kiertoakselin A suhteen? Ilmoita vastaus kahden merkitsevän numeron tarkkuudella. Huomioi momentin merkki.
Nm
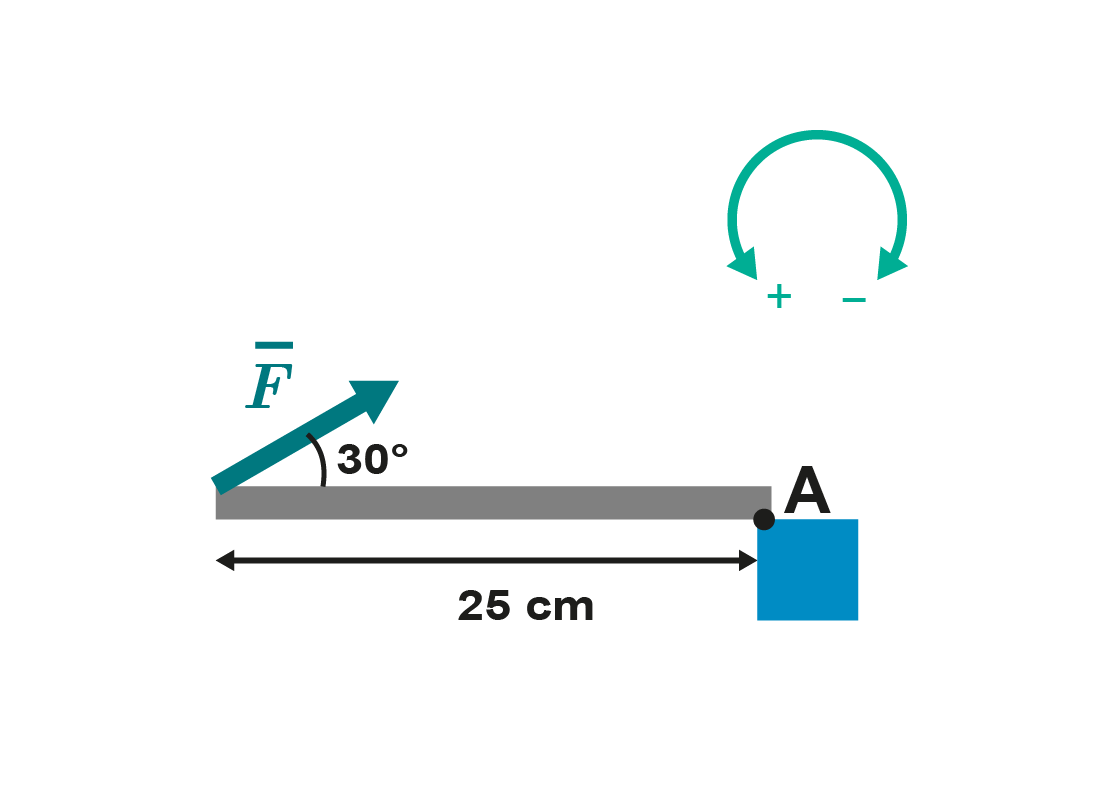
5. Voiman suuruus on 10 N. Kuinka suuri on voiman momentti kiertoakselin A suhteen? Ilmoita vastaus kahden merkitsevän numeron tarkkuudella. Huomioi momentin merkki.
Nm

What would you like to do with the text? The text is processed by artificial intelligence, it is not checked or edited! The text may contain errors. Check the accuracy of the text against the original text in the textbook.
Choose the files you want to add. Supported formats are txt, html, htm, pdf, odt, odp, ods, xls, xlsx, ppt, pptx, pps, doc, docx, rtf, png, jpg, jpeg and gif.
| Name | |
|---|---|
| remove |
NB! Links must begin with: “http://”!
Opiq uses essential cookies to make our website work, to help keep you safe, to analyse user interaction and to improve user experience.
Cookie is a small file which is sent from users computer to the website server. It includes necessary information for the website to operate and includes information about the user and their preferences.
Most of the cookies are necessary for the operation of Opiq. It is possible to deny analytical cookies and in that case your usage data is not used to develop and improve Opiq services. Read more