Let us examine the photoelectric effect from the perspective of the quantum hypothesis presented above and the law of conservation of energy. Radiation transfers energy to the metal in individual quanta. If the frequency is low, the energy of the quanta is so small that it cannot release electrons. Increasing the frequency of the radiation increases the energy of the quanta until the energy is sufficient to release electrons.
The threshold frequency at which electrons begin to be emitted is different for each metal. At the threshold frequency, the energy of the quanta is equal to the work function, , characteristic of the metal. The values of work functions for different metals can be found in science tables. If the frequency of the radiation is higher than the threshold frequency, part of the energy of the quanta is converted into the kinetic energy
E
k
of the emitted electrons.
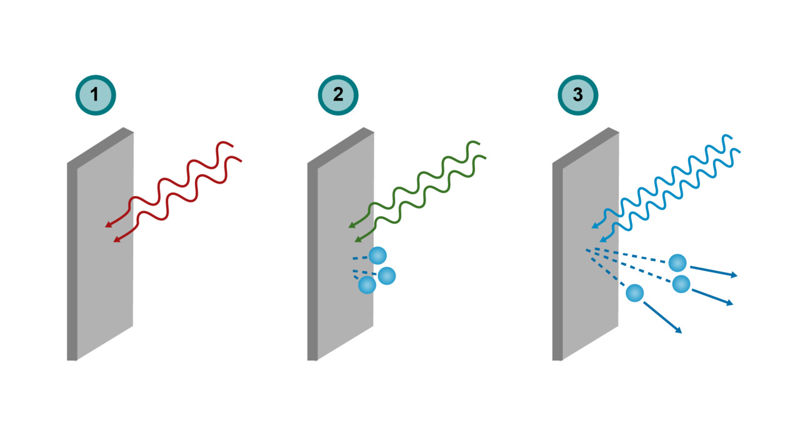
The image series presents the interaction between a metal plate and radiation of three different frequencies.
- Low-frequency radiation does not produce the photoelectric effect.
- At the threshold frequency, electrons are released and the photoelectric effect occurs, but the released electrons have no kinetic energy.
- At high frequency, emitted electrons have kinetic energy.
Quanta of electromagnetic radiation
The energy of electromagnetic radiation appears in packets called quanta. Radiation is absorbed or emitted one quantum at a time. Whether the photoelectric effect occurs depends on the energy of the quantum.
Conservation of energy in the photoelectric effect
The conservation of energy in the photoelectric effect can be expressed with the following equation:
E
quantum
=
W
0
+
E
k
The energy of the quantum is converted into the work function and the kinetic energy of the electrons. The equation above is often written in a form where the kinetic energy of the electrons is calculated as the difference between the energy of the quantum and the work function.
E
k
=
E
quantum
−
W
0
Work done by the electric field and kinetic energy
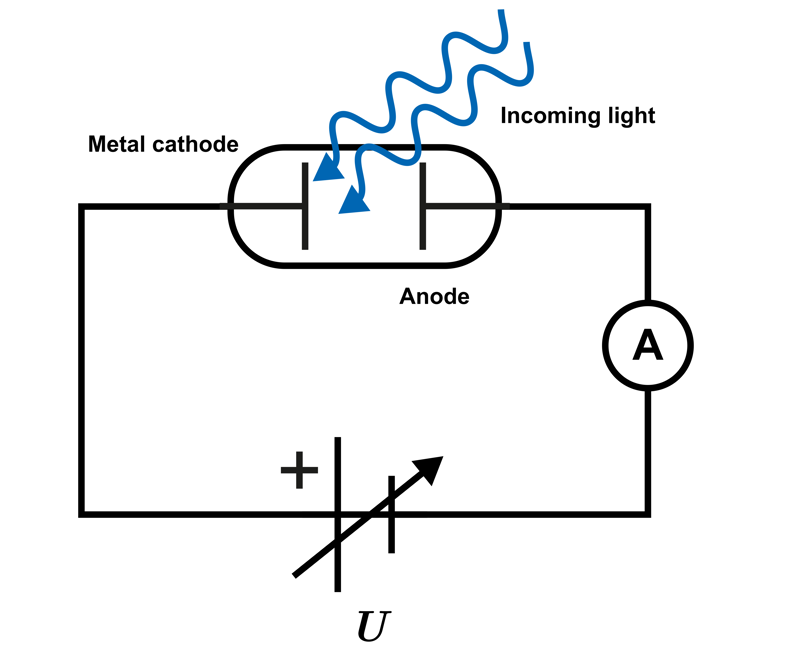
The above equation can be derived in an experiment where light is directed onto a metal plate and the energy of the emitted electrons is determined. A suitable circuit for this is shown in the accompanying diagram.
The cathode and anode are placed in a vacuum tube where the emitted electrons generate an electric current in the circuit. The current can be stopped by connecting a stopping voltage
U
between the anode and cathode, producing an electric force that opposes the motion of the electrons emitted from the cathode. In this case, the electric field does the work required to stop the motion of the electrons.
Work done by the electric field:
W
=
F
s
=
Q
E
s
=
Q
U
In the experiment, the stopping voltage is adjusted so that the electric current in the circuit ceases.
Radiation of different frequencies is directed at the cathode, and the maximum kinetic energy of the emitted electrons is determined. Once the threshold frequency is exceeded, the kinetic energy of the electrons is observed to increase as the frequency increases. The magnitude of the kinetic energy can be determined when the electric current just ceases. At that point, the work done by the electric field is equal to the kinetic energy of the electrons
Q
U
=
E
k
.
Electronvolt as a unit
When the stopping voltage is
U
the maximum energy of the emitted electrons is
Q
U
, where
Q
is the charge of the electron, i.e. the elementary charge. When the elementary charge is denoted by the symbol e, the energy of the electrons is expressed in the unit eV (electronvolt).
The basic unit of energy, the joule (J), is quite large compared to the energies of radiation quanta. It is often more practical to use the unit of energy called the electronvolt. When an electron is accelerated in an electric field with a voltage of 1 V, the energy gained through the work done by the electric field is
1
V
⋅
1
e
=
1
e
V
. A proton, that has the same amount of charge, would also gain an energy of 1 eV in the corresponding situation.
The conversion factor between the joule and the electronvolt is the numerical value of the elementary charge in coulombs, i.e. the following conversion applies between them:
1
eV
=
1.602
176462
⋅
10
−
19
J
Investigating the photoelectric effect
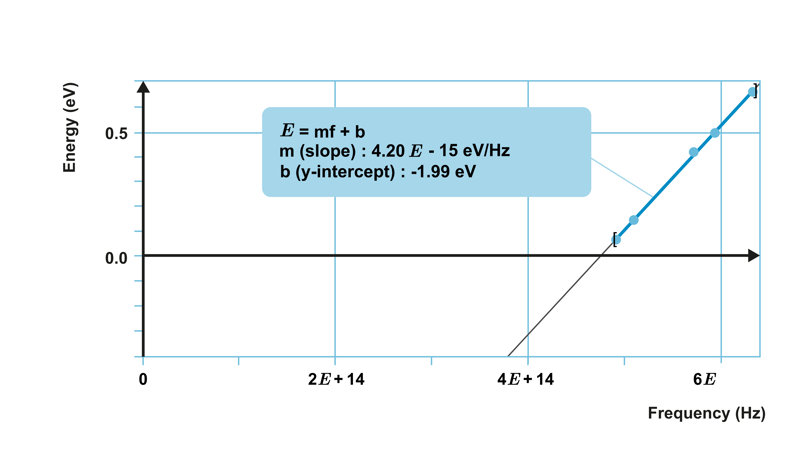
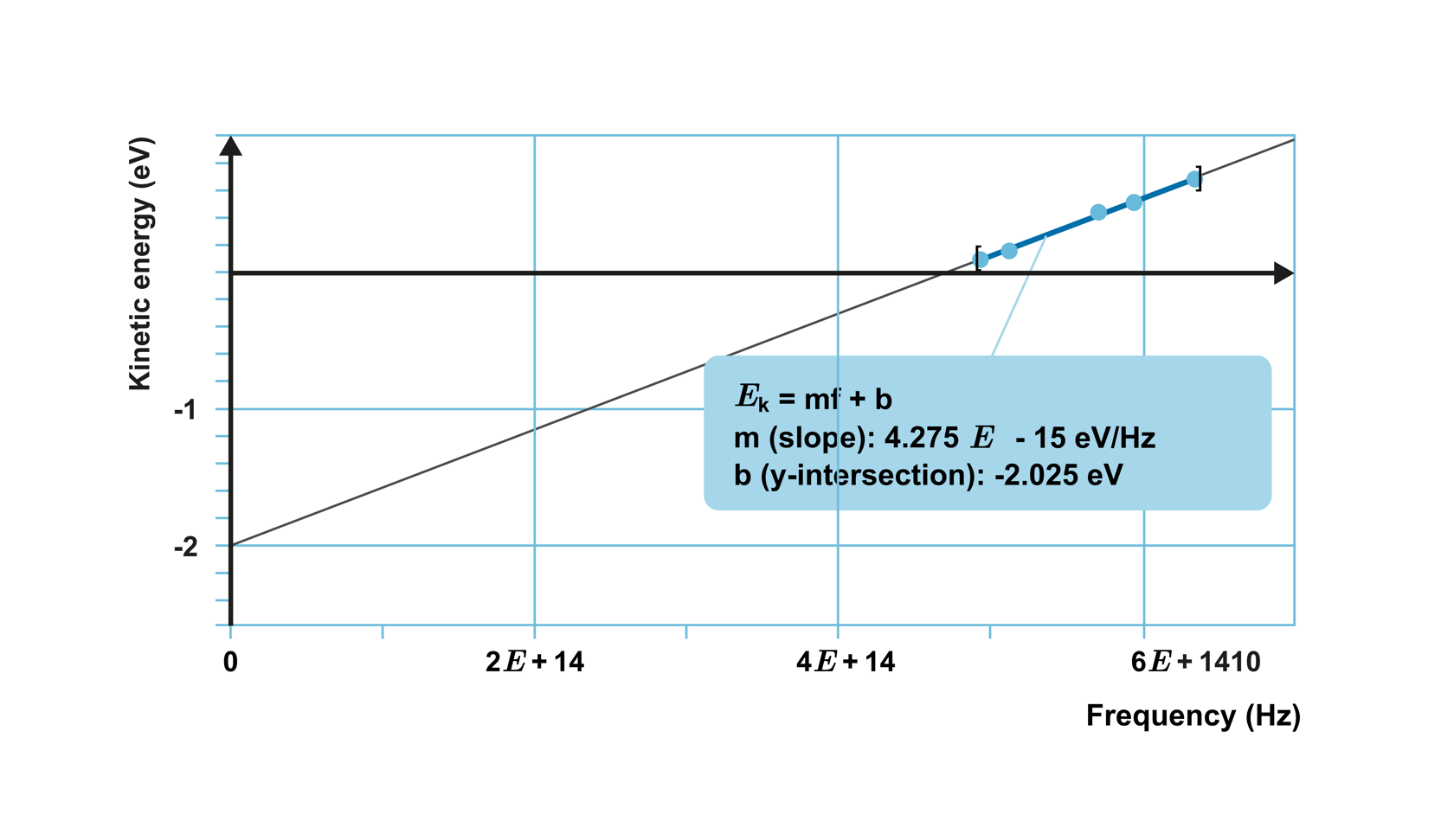
When investigating the photoelectric effect with a certain metal, a relationship was observed between the maximum kinetic energy of the emitted electrons and the frequency of the light, as shown in the graph below.
The points lie on a straight line, which means that the kinetic energy of the electrons increases linearly as the frequency increases. The equation of the straight line is obtained as
E
k
=
constant
⋅
f
−
W
0
,
where constant represents the slope of the line and
W
0
is the y-intercept of the line.
By repeating the experiment with different metals, it is observed that the measurement points always lie on a straight line with the same slope, but with varying
W
0
.
The slope is called Planck’s constant, and marked with
h
. It can be expressed in units of Js or eVs, and it's exact value is
h
=
6.626
06957
⋅
10
−
34
Js
=
4.135
66751
⋅
10
−
15
eVs
The constant
W
0
represents the work function characteristic of each metal. In the graph shown below, its value is -1.99 eV.
Interpretation of the photoelectric effect
The photoelectric effect can be interpreted as follows: In the phenomenon, a quantum of electromagnetic radiation transfers all oiits energy to an electron in the metal. Part of the energy is used for the work function
W
0
. The remaining energy is converted into the kinetic energy
E
k
of the electron.
E
quantum
=
E
k
+
W
0
This formula should always be justified from the perspective of the principle of conservation of energy whenever it is used.
Quantum energy
The energy of a radiation quantum, as presented in the previous context, can be written as the product of Planck’s constant
h
and the frequency of the radiation
f
:
E
quantum
=
h
f
h
=
6.626
06957
⋅
10
−
34
Js
=
4.135
66751
⋅
10
−
15
eVs
According to the basic equation of wave motion
f
=
c
λ
, so the energy of a quantum can also be calculated using the wavelength
λ
, the speed of light
c
and Planck’s constant
h
:
E
quantum
=
h
c
λ
The energy of a radiation quantum is expressed either in joules or electronvolts. The unit of energy depends on which unit is used for Planck’s constant.
1. The energy of the electromagnetic radiation quantum is not sufficient to detach an electron from the metal plate. What should be done?
Increase the intensity of the radiation.
Increase the wavelength of the radiation.
Wait.
Increase the frequency of the radiation.
2. The frequency of the electromagnetic radiation is equal to the threshold frequency of a certain metal.
The energy of the radiation quantum is not sufficient to detach electrons from the metal plate.
The energy of the radiation quantum is sufficient to detach electrons from the metal plate, but the emitted electrons have no kinetic energy.
The energy of the radiation quantum is sufficient to detach electrons from the metal plate, and the emitted electrons have kinetic energy.